The vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.Solution in Bengali
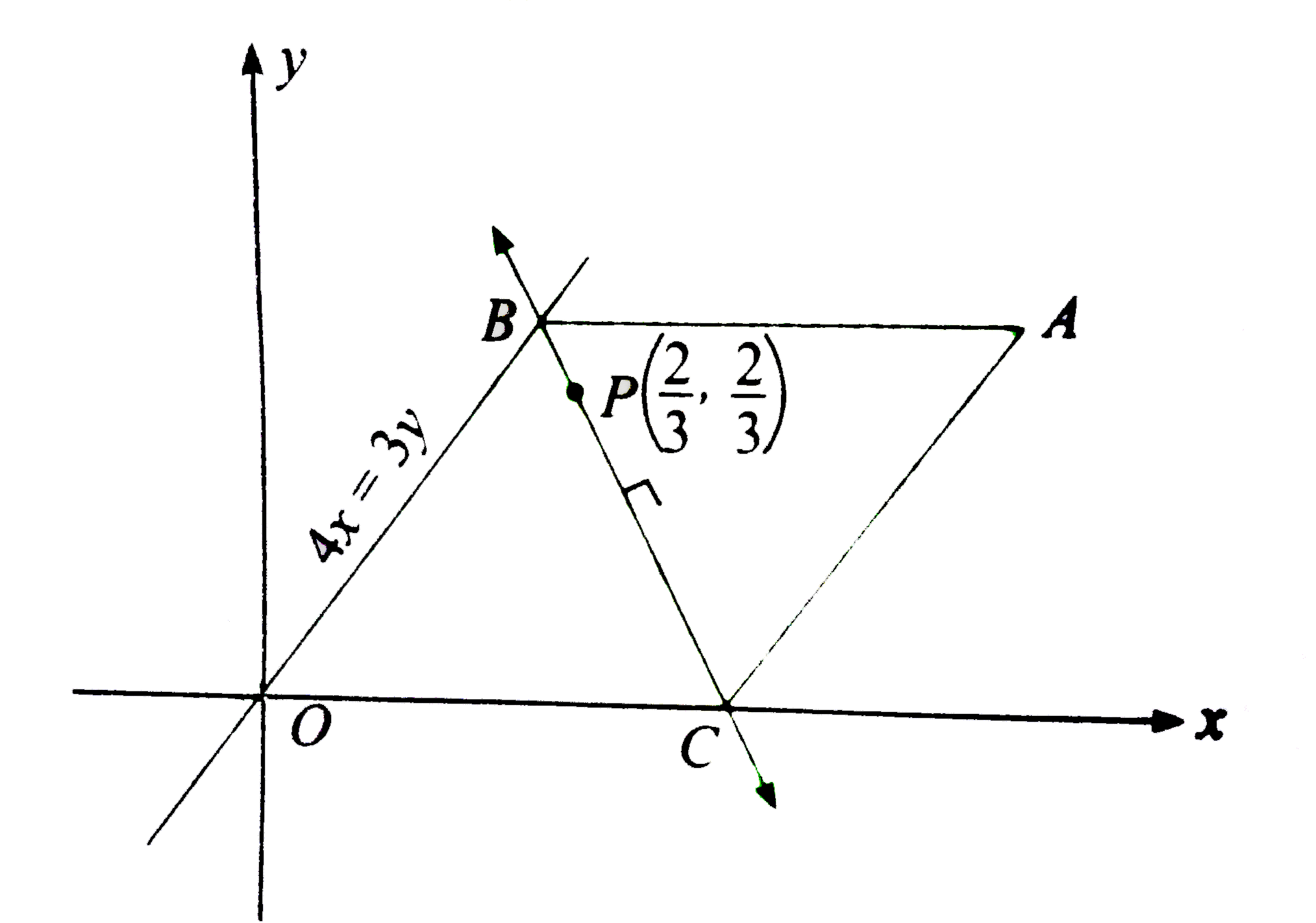
Diagonals of rhombus are equally inclined to the sides.
So, diagonals are parallel to or coincident with the angle bisectors of sides.
Equations of bisectors of sides OC and OB of rhombus are
4x−3y5=±y1
or x-2y=0 and 2x+y=0
Clearly, diagonal BC is parallel to the bisector 2x+y=0.
So, equation BC is
y−23=−2[x−23]
or 2x+y-2=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE
12 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
23 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
View SolutionFind the equation of the right bisector of the line segment joining the points (3,4) and (-1,2).
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionThe vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.
View SolutionThe base of the pyramid AOBC is an equilateral triangle OBC with each side equal to 4√2,O is the origin of reference, AO is perpendicualar to the plane of OBC and ∣∣→AO∣∣=2. Then find the cosine of the angle between the skew straight lines, one passing though A and the midpoint of OBand the other passing through O and the mid point of BC.
View SolutionThe vertices B and C of a triangle ABC lie on the lines 3y=4x and y=0 respectively and the side BC passes through the point ((2)/(3),(2)/(3)) If ABOC is a rhombus,o being the origin.If co-ordinates of vertex A is (alpha,beta), then find the value of (5)/(2)(alpha+beta)
View SolutionIf sides of triangle ABC are a,bandc such that 2b=a+c then bc>23 (b) bc>13 bc<2 (d) bc<32
View SolutionThe vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionIn a triangle ABC , the bisectors of angles BandC lies along the lines x=yandy=0. If A is (1,2) , then the equation of line BC is (a) 2x+y=1 (b) 3x−y=5 (c) x−2y=3 (d) x+3y=1
View SolutionThe base of the pyramid AOBC is an equilateral triangle OBC with each side equal to 4√2,O is the origin of reference, AO is perpendicualar to the plane of OBC and ∣∣→AO∣∣=2. Then find the cosine of the angle between the skew straight lines, one passing though A and the midpoint of OBand the other passing through O and the mid point of BC.
View SolutionThe vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.
View SolutionThe sides ABandAC of a triangle ABC are respectively 2x+3y=29andx+2y=16 respectively. If the mid-point of BCis(5,6) then find the equation of BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.
View Solution
