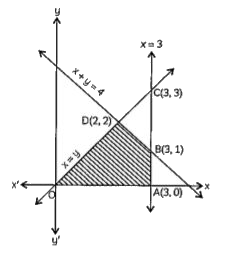
The vertices of a closed - convex polygon representing the feasible region of the objective function f are (4,0), (2,4),(3,2) and (1,4) . Find the maximum value of the objective function f=7x+8y.
A
39
B
46
C
49
D
38
Video Solution
Text Solution
The correct Answer is:B
(i) Substitute the given points.
(ii) The maximum/ minimum value of f occurs at one of the vertices of the closed - convex polygon.
(iii) Substitute the given point in f.
(iv) Identify the maximum value of f.
|
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Level 3
10 Videos
- LINEAR PROGRAMMINGBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Level 1
15 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
- LOGARITHMSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 3
15 Videos
Similar Questions
Knowledge Check
The vertices of a closed - convex polygon representing the feasible region of the objective function f =5x+3y , are (0,0),(3,0),(3,1),(1,3) and (0,4) . Find the maximum value of the objective function.
A6B18C14D15The vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y
A61B69C59D49The vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y
A64B79C94D87
The corner points of the feasible region of an LPP are (0,0),(0,8),(2,7),(5,4) and (6,0). The maximum value of the objective function Z = 3x + 2y is:
View SolutionIf the vertices of a closed - convex polygon are A(8,0), O(0,0), B (20,10), C(24,5) and D(16,20), then find the maximum value of the objective function f=14x+15y.
View SolutionConsider the function f(x)=0.75x4−x3−9x2+7
What is the maximum value of the function?
View SolutionThe corner point of the feasible solutions are(0,0) (3,0)(2,1)(0,7/3) the maximum value of Z= 4x+5y is
View SolutionIn the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
View Solution
