The vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.Solution in Bengali
The angle bisector of ∠B meets the opposite side in D.
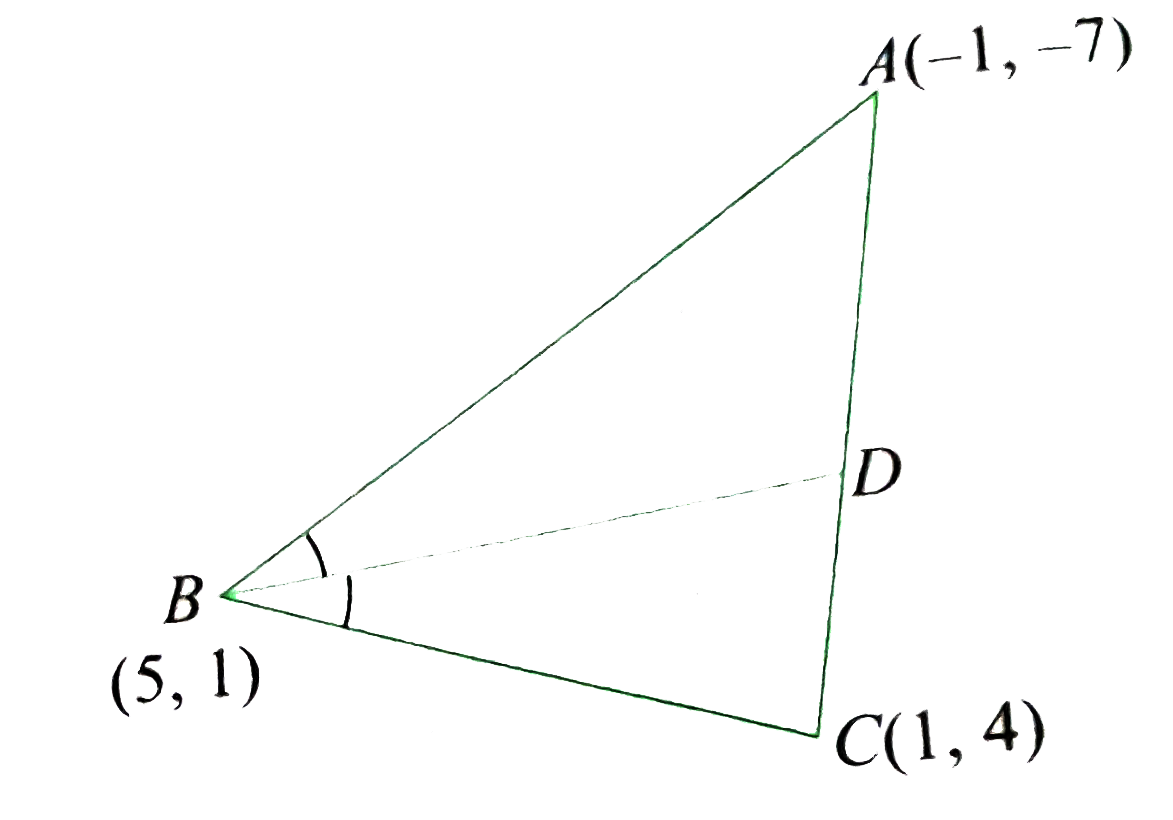
Using angle bisector theorem , we have
AD:DC=AB:BC
Now, AB=√(5+1)2+(1+7)2=10
and BC=√(5−1)2+(1−4)2=5
∴D=(2(1)+1(−1)2+1,2(4)+1(−7)2+1)=(13,13)
∴BD=√(5−13)2+(1−13)2=10√23
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.38
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.39
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.36
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Determine x so that the line passing through (3,4)and(x,5) makes an angle of 1350 with the positive direction of the x-axis.
View SolutionWhich line is having the greatest inclination with the positive direction of the x-axis?
(i) Line joining the points (1, 3) and (4, 7)
(ii)Line 3x−4y+3=0
View SolutionIf a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid of the triangle.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionThe vertices of a triangle are (A(−1,−7),B(5,1), and C(1,4). The equation of the bisector of ∠ABC is____
View SolutionThe vertices of a triangle are A(-1,-7),B(5,1) and C(1,4). The equation of the bisector of the angle ABC
View SolutionThe vertices f the triangle are A(5,4,6), B(1,−1,3)nad C(4,3,2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.
View SolutionA(1,3,0),B(2,2,1) and C(5,−1,4) are the vertices of the triangle ABC, if the bisector of ∠BAC meets its side ¯¯¯¯¯¯BC at D, then find the coordinates of D.
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionThe vertices of a triangle are (A(−1,−7),B(5,1), and C(1,4). The equation of the bisector of ∠ABC is____
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionFind the equation of the bisector of angle A ofthe triangle whoe vertices are A(4,3),B(0,0)andC(2,3).
View SolutionABC is a triangle in which ∠A=720, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC
View Solution
