The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1), (1, 1) and (1, 0) is Solution in Bengali
The correct Answer is:B
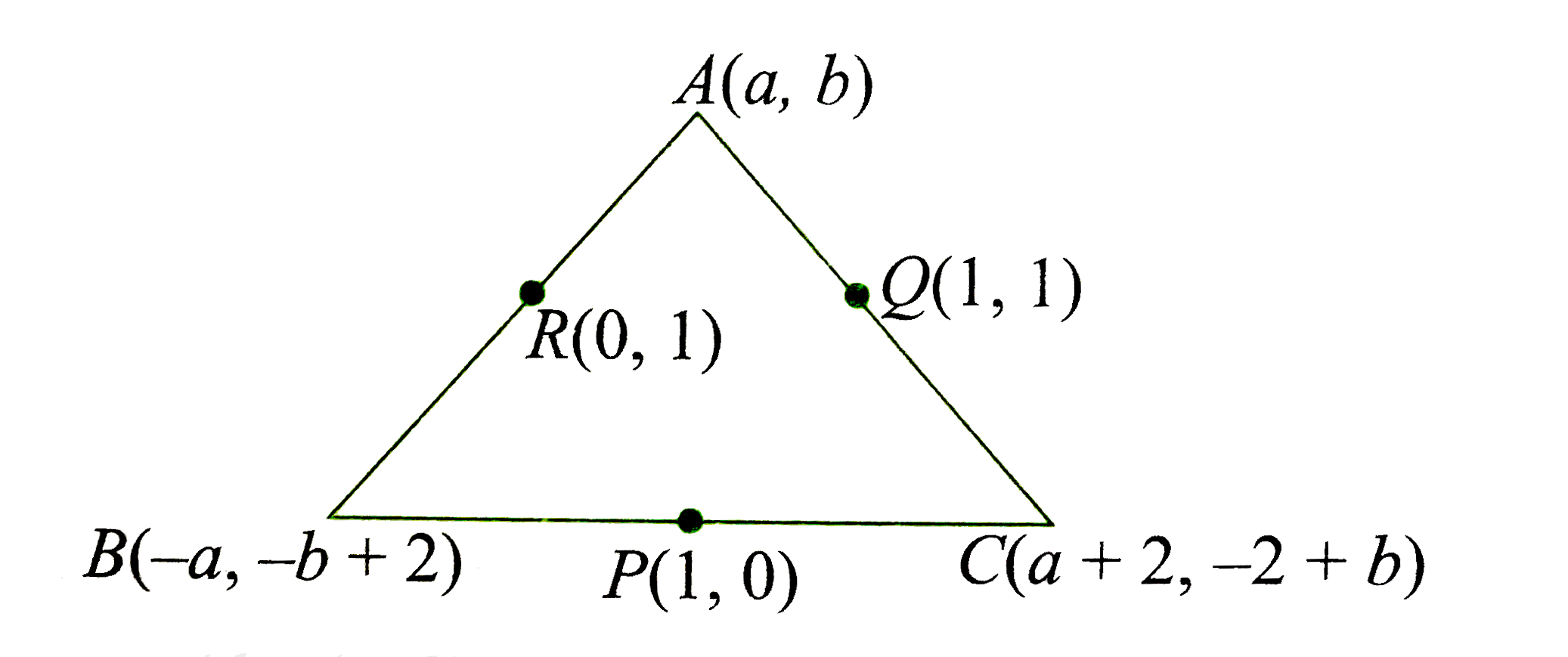
Let vertex A be (a, b).
R is mid point of AB.
Pis mid point of BC.
Q is mid point of AC.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (JEE ADVANCED)3videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (NUMERICAL VALUE TYPE)13videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
The locus of the orthocentre of the triangle formed by the lines (1+p)x−py+p(1+p)=0,(1+q)x−qy+q(1+q)=0 and y = 0, where p≠⋅q, is (A) a hyperbola (B) a parabola (C) an ellipse (D) a straight line
03:22View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
02:57View SolutionFind the number of permutations of the set {1,2,3,4} in which no two adjacent positions are filled by consecutive integers ( increasing orders).
02:08View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
06:59View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
03:45View Solutionif the coordinates of the mid points of the sides of a triangle are (1,2),(0,-1) and (2,-1). Find the coordinates of its vertices ':
20:45View SolutionIf the points (1,-1), (2,-1) and (4,-3) are the mid points of the sides of a triangle then write the coordinates of its centroid.
14:39View SolutionIf (1,2),(0,−1)and(2,−1) are the middle points of the sides of a triangle, find the coordinates of its centroid.
01:47View SolutionThe mid-points of the sides of a triangle are (12,0),(12,12)and(0,12). Find the coordinates of the incentre.
03:28View SolutionThe mid-points of the sides of a triangle are (1, 2), (0,-1) and (2, -1). Find the coordinates of the vertices of a triangle with the help of two unknowns.
06:18View SolutionThe coordinates of the mid-points of the sides of a triangle are ( 4 , 3, 4) , ( 1, 5 , -1) and ( 0 , 4 , - 2) , find the coordinates of the vertices of the triangle .
06:36View SolutionThe coordinates of the mid-points of the sides of a triangle are ( 3 , - 1 , -1) , ( 1 , 3 , - 4) and ( 0 , 1 , - 2) , find the coordinates of the vertices .
03:04View SolutionIf the coordinates of the mid-points of the sides of a triangle are (1, 1) , (2, -3) and (3, 4). Find the coordinates of the centroid.
10:36View SolutionThe x-coordinate of the incentre of the triangle where the midpoints of the sides are (0, 1) (1, 1) and (1, 0) is
09:30View SolutionIf the coordinates of the mid points of the sides of a triangle are (1,2) , (0,-1) and (2,-1) . Find the coordinates of its vertices :
06:32View SolutionIf (0, 1), (1, 1) and (1, 0) are the mid points of the sides of a triangle, the coordinates of its incentre are
10:58View Solution

