There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
To determine which of the two cuboidal boxes requires less material to make, we need to calculate the total surface area of each box. The box with the lesser surface area will require less material.
Step 1: Calculate the Surface Area of Box A (Cuboid)
The formula for the total surface area (TSA) of a cuboid is given by:
TSA=2(lb+bh+hl)
where l is the length, b is the breadth, and h is the height.
For Box A:
- Length (l) = 60 cm
- Breadth (b) = 40 cm
- Height (h) = 50 cm
Substituting the values into the formula:
TSA=2(60×40+40×50+50×60)
Calculating each term:
- 60×40=2400
- 40×50=2000
- 50×60=3000
Now, substituting these values back into the TSA formula:
TSA=2(2400+2000+3000)=2(7400)=14800 cm2
Step 2: Calculate the Surface Area of Box B (Cube)
The formula for the total surface area of a cube is given by:
TSA=6×side2
For Box B:
- Side = 50 cm
Substituting the value into the formula:
TSA=6×(50)2
Calculating:
(50)2=2500
So,
TSA=6×2500=15000 cm2
Step 3: Compare the Surface Areas
- Surface Area of Box A = 14800 cm²
- Surface Area of Box B = 15000 cm²
Since 14800 cm² < 15000 cm², Box A requires less material to make.
Conclusion
The cuboid in Figure A requires less material than the cube in Figure B because it has a lesser surface area.
---
TSA=2(lb+bh+hl)
where l is the length, b is the breadth, and h is the height.
- Length (l) = 60 cm
- Breadth (b) = 40 cm
- Height (h) = 50 cm
TSA=2(60×40+40×50+50×60)
- 60×40=2400
- 40×50=2000
- 50×60=3000
TSA=2(2400+2000+3000)=2(7400)=14800 cm2
TSA=6×side2
For Box B:
- Side = 50 cm
TSA=6×(50)2
Calculating:
(50)2=2500
So,
TSA=6×2500=15000 cm2
- Surface Area of Box B = 15000 cm²
The cuboid in Figure A requires less material than the cube in Figure B because it has a lesser surface area.
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.2
11 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 11.1
5 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - EXERCISE 2.3
9 Videos
- PLAYING WITH NUMBERSBOOK - NCERT ENGLISHCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 16.1
10 Videos
Similar Questions
A ray falls on a prism ABC(AB=BC) and travels as shown in adjoining figure.The minimum refraction index of the prism material should be -
View SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . Which of the following option is correct

View Solution
Knowledge Check
In the adjoining figure, the value of x that will make AOB a straight line is
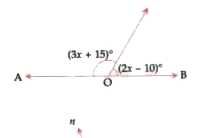 Ax=40Bx=35Cx=30Dx=25
Ax=40Bx=35Cx=30Dx=25In the adjoining figure, the value of x that will make AOB a straight line is
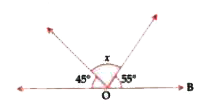 A60∘B70∘C80∘D100∘
A60∘B70∘C80∘D100∘
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.(i) Which box has the greater lateral surface area and by how much? (ii) Which box has the smaller total surface area and by how much?
View SolutionA force if 15N acts on a box as shown in (figure).What are the horizontal component and vertical components of force?
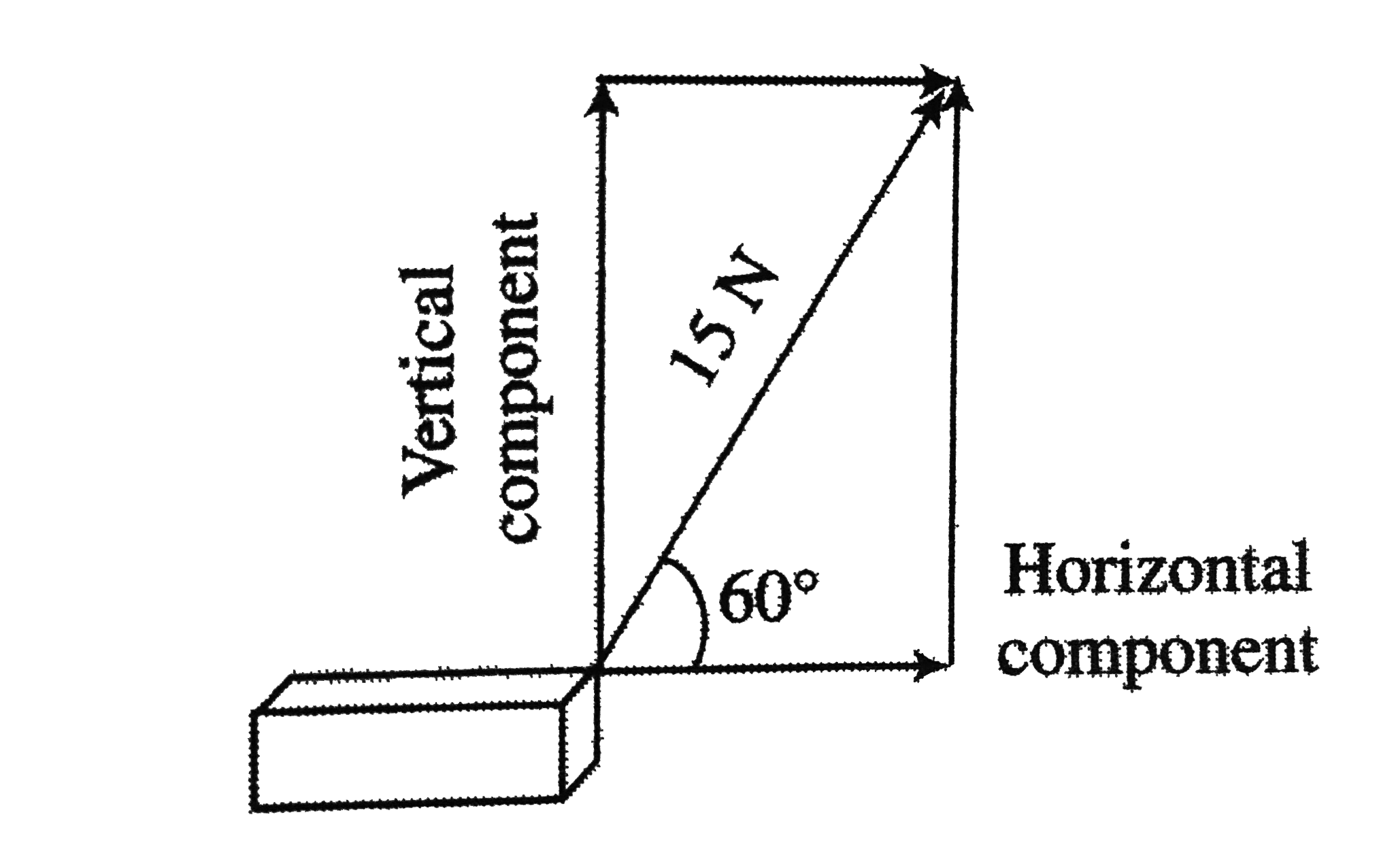
View SolutionA turck is moving on the ground with a velocity v=12m/s and a box is moving on the truck with respect to it with a velocity u=5m/s as shown in the figure. What is the velocity of the box with respect to the ground?

View SolutionA box 3 m long. 62.5 cm wide and 65 cm deep is to be made . It is to be open at the top. Ignoring the thickness of the sheet of which box is made. Determine :
area of the sheet required to make the box.
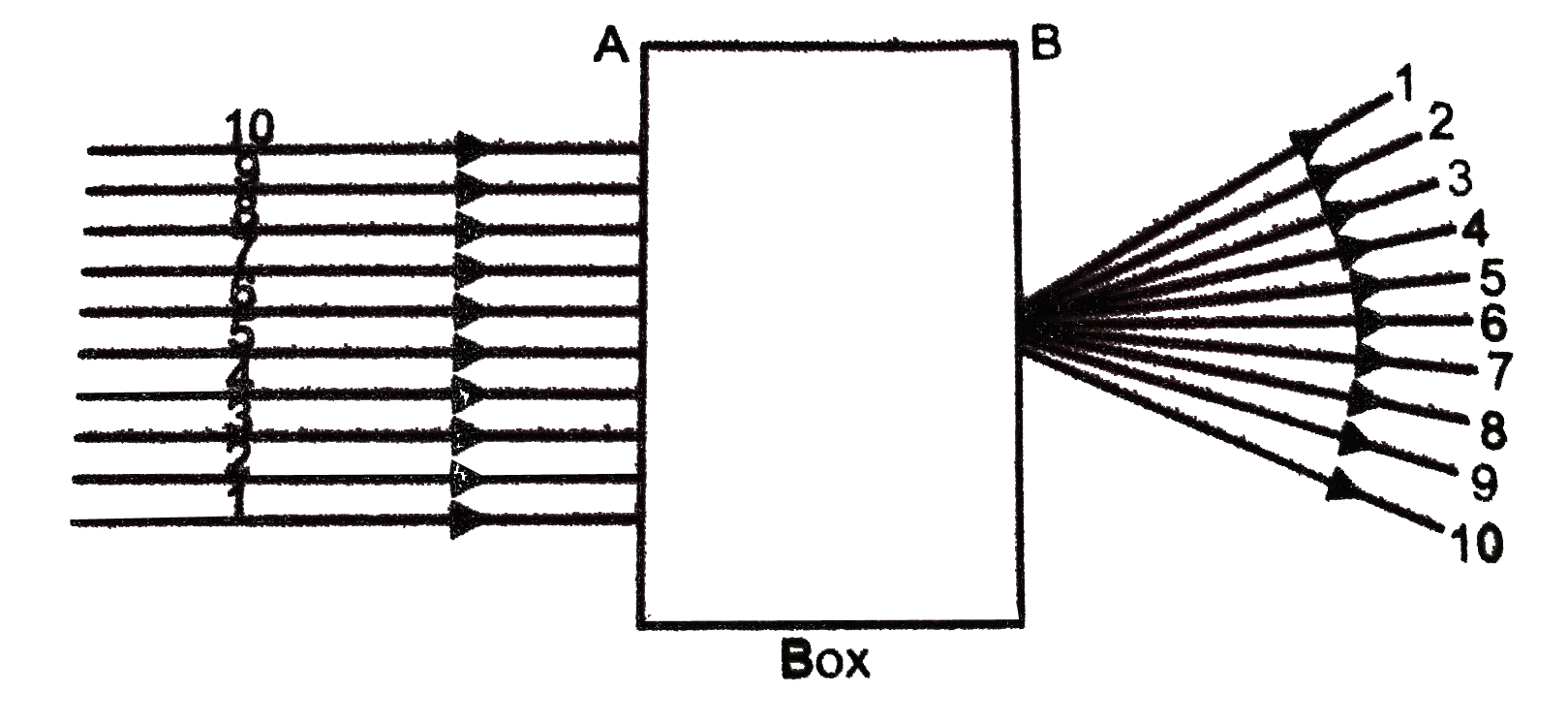
View SolutionA beam of light is incident through the holes on side A and emerges out of the holes on the other face of the box as shown in Figure. Which of the following could be inside the box ?
View SolutionA box is falling freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle θ as shown in the figure.
Assertion (A) : The path of the particle with respect to an oberver sitting in the box will be a straight line.
Reasoning (R ) : The acceleration of particle with respect to the box is zero. Then,

View Solution
