Three identical spherical balls fit snugly into a cylindrical can. The radius of each of the spherical ball equals the radius of the can and the balls just touch the bottom and the top of the can. What fraction of the volume of the can is taken up by the balls?
35
43
32
23
The correct Answer is:D
Step by step video, text & image solution for Three identical spherical balls fit snugly into a cylindrical can. The radius of each of the spherical ball equals the radius of the can and the balls just touch the bottom and the top of the can. What fraction of the volume of the can is taken up by the balls? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - EVERYDAY MATHEMATICS10videos
IMO QUESTION PAPER 2018 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2018 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2017 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2018 SET B
Similar Questions
Three metallic spherical balls of radii 3 cm, 4 cm and 5 cm are melted and recast into a big spherical ball. Find the radius of this big ball.
View SolutionA cylindrical rod of iron whose radius is one-fourth of its height is melted and cast into spherical balls of the same radius as that of the cylinder. What is the number of spherical balls ?
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical box of radius 5 cm contains 10 solid spherical balls, each of radius 5 cm. If the top most ball touches the upper cover of the box, then volume of the empty space in the box is
A25003πcm3B5000πcm3C2500πcm3D50003πcm3 - Question 2 - Select One
N solid metalic spherical balls are melted and reast into a cylindrical rod whose radius is 3 times that of a spherical ball and height is 4 times the radius of a spherical ball. The value of N is
A30B24C36D27 - Question 3 - Select One
A spherical ball of lead 6 cm in radius is melted and recast into three spherical balls. The radii of two of these balls are 3cm and 4 cm. What is the radius of the third sphere ?
A4.5 cmB5 cmC6 cmD7 cm
A spherical ball of lead has been melted and meade in to smaller balls of half the radius of the original one. How many balls can be made?
View SolutionA spherical metal ball of radius 8 cm is melted to make 8 smaller identical balls. The radius of each new ball is cm.
View SolutionThe diameter of hollow cone is equal to the diameter of a spherical ball. If the ball is placed at the base of the cone, what portion of the ball will be outside the cone –
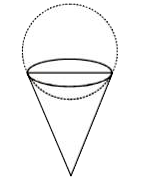
View SolutionThere are two identical spherical balls of same material one being solid and the other being hollow. Then they can be distinguished by
View SolutionA spherical ball of lead 6 cm in radius is melted and recast into three spherical balls. The radii of two of these balls are 3cm and 4 cm. What is the radius of the third sphere ?
View Solution