Through which of the following point , the graph of y=-x passes?
(1,1)
(0,1)
(-1,1)
(0,0)
The correct Answer is:C
To determine through which points the graph of the equation y=−x passes, we can evaluate each given point by substituting the x-coordinate into the equation and checking if the resulting y-coordinate matches.
1. Understand the Equation: The equation y=−x means that for any value of x, y will be the negative of that value. This indicates a straight line that passes through the origin (0, 0) and has a slope of -1.
2. Evaluate Each Point: We will check each point provided to see if it satisfies the equation y=−x.
- Point 1: (1, 1)
- Substitute x=1:
y=−1
- The point (1, 1) does not satisfy the equation since y should be -1, not 1.
- Point 2: (0, 1)
- Substitute x=0:
y=−0=0
- The point (0, 1) does not satisfy the equation since y should be 0, not 1.
- Point 3: (-1, 1)
- Substitute x=−1:
y=−(−1)=1
- The point (-1, 1) satisfies the equation since y is indeed 1 when x is -1.
- Point 4: (0, 0)
- Substitute x=0:
y=−0=0
- The point (0, 0) satisfies the equation since y is 0 when x is 0.
3. Conclusion: The points through which the graph of y=−x passes are:
- (-1, 1)
- (0, 0)
Final Answer:
The graph of y=−x passes through the points (-1, 1) and (0, 0).
- Substitute x=1:
y=−1
- The point (1, 1) does not satisfy the equation since y should be -1, not 1.
- Substitute x=0:
y=−0=0
- The point (0, 1) does not satisfy the equation since y should be 0, not 1.
- Substitute x=−1:
y=−(−1)=1
- The point (-1, 1) satisfies the equation since y is indeed 1 when x is -1.
- Substitute x=0:
y=−0=0
- The point (0, 0) satisfies the equation since y is 0 when x is 0.
- (-1, 1)
- (0, 0)
The graph of y=−x passes through the points (-1, 1) and (0, 0).
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICES QUESTION PAPER -3EXERCISE - PART A(Fill in the blank)1videos
PRACTICES QUESTION PAPER -3
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICES QUESTION PAPER -3EXERCISE - PART B8videos
PRACTICES QUESTION PAPER -3
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST QUESTION PAPER 1EXERCISE - SECTION-D5videos
PRACTICE TEST QUESTION PAPER 1
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST6videos
PROBABILITY MIND MAP
Similar Questions
The graph of (y−x) against (y+x) is shown below.
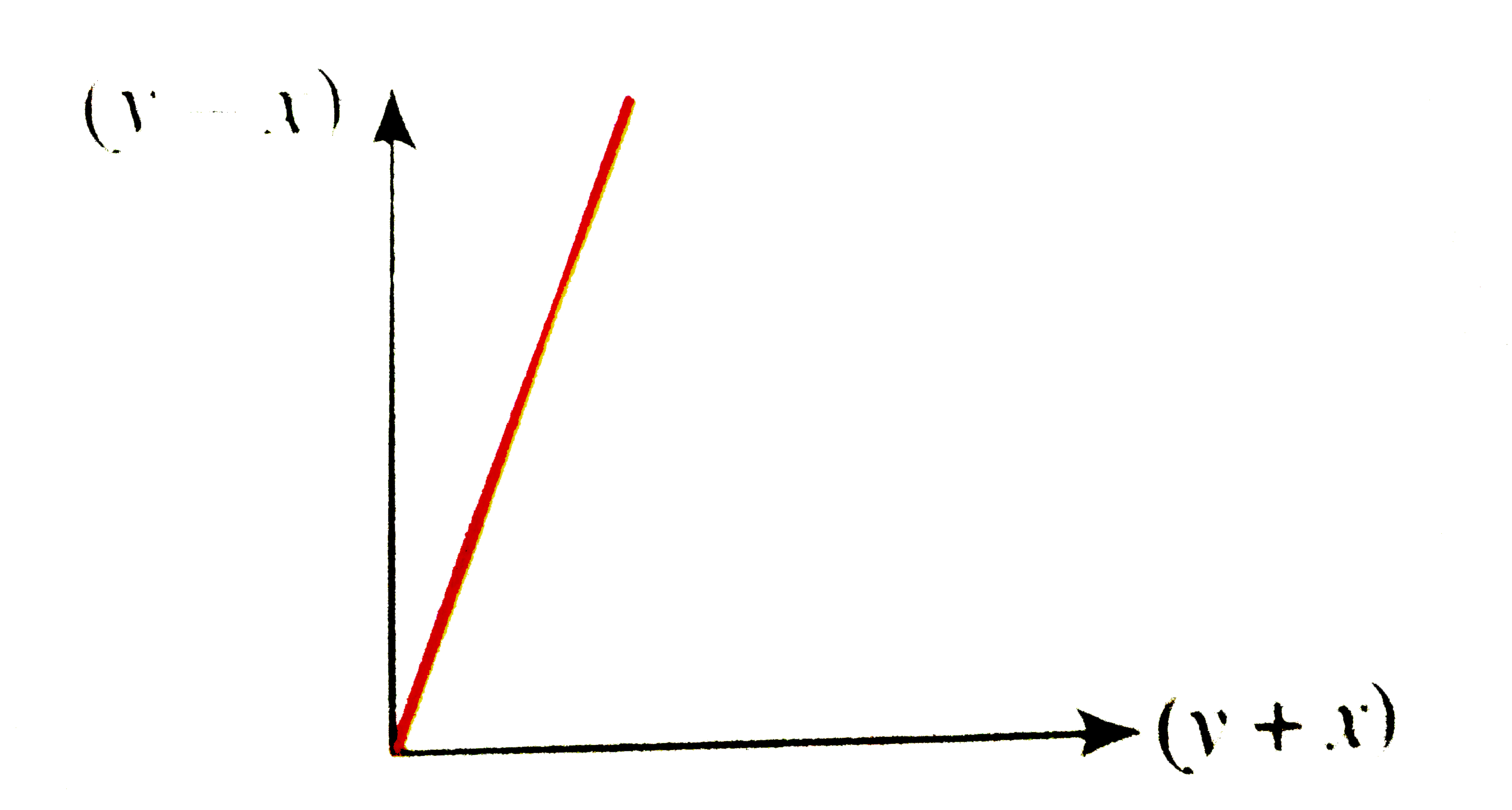
Which one of the following shows the graph of y against x ?
 View Solution
View SolutionP(1,1) be a point and x2+y2+2x+2y−8=0 be circle such that chord AB passing through P satisfies PAPB=√5−2√5+2 then which of the following point lies on line passing through line passing A and B.
View Solution
Knowledge Check
- Question 1 - Select One
A curve f(x)=x2+ax−b pass through p(1,−5) and tangent to f(x) at point p is perpendicular to x−y+5=0 then which of the following point will lie on curve ?
A(2−2)B(2−1)C2,−1)D(−2,2) - Question 2 - Select One or More
y = f(x) which has differential equation y(2xy+ex)dx−exdy=0 passing through the point (0,n 1). Then which of the following is/are true about the function?
Ax=1+√2 is point of local maximaBx=1−√2 is point of local minimaClimx→∞f(x)=−∞Dlimx→−∞f(x)=0 - Question 3 - Select One
The equation of tangent to the parabola y2=9x, which pass through the point (4, 10) is
Ax+4y+1=0B9x+4y+4=0Cx−4y+36=0D19x−14y+4=0
Find the equations of the circles which pass through the common points of the following pair ofcircles.(a)x2+y2+2x+3y−7=0 and x2+y2+3x–2y−1=0 through the point (1,2)
View SolutionFind the equation of the line through the point of intersection of x+2y=5andx−3y=7 and passing through the point (0,−1)
View SolutionThe graph of y =x passes through the point
View SolutionThe graph of the line y=3 passes through the point
View SolutionThe graph of the line x=3 passes through the point
View Solution

