TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
No
Yes
Cannot say
Data insufficient
The correct Answer is:B
Step by step video, text & image solution for TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT SHEET - 24
10 Videos
- AVERAGEBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET
10 Videos
- CO-ORDINATE GEOMETRYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Self Assessment Sheet
10 Videos
Similar Questions
Prove that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View SolutionIn a given figure, TQ and TP are tangents on bigger circle with centre O and TP & TR are tangents on smaller circle with O' then find the ratio of TQ : TR?

View Solution
Knowledge Check
TP and TQ are the tangents to a circle, with centre O. Find x.
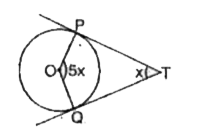 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A200∘B160∘C100∘D80∘
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
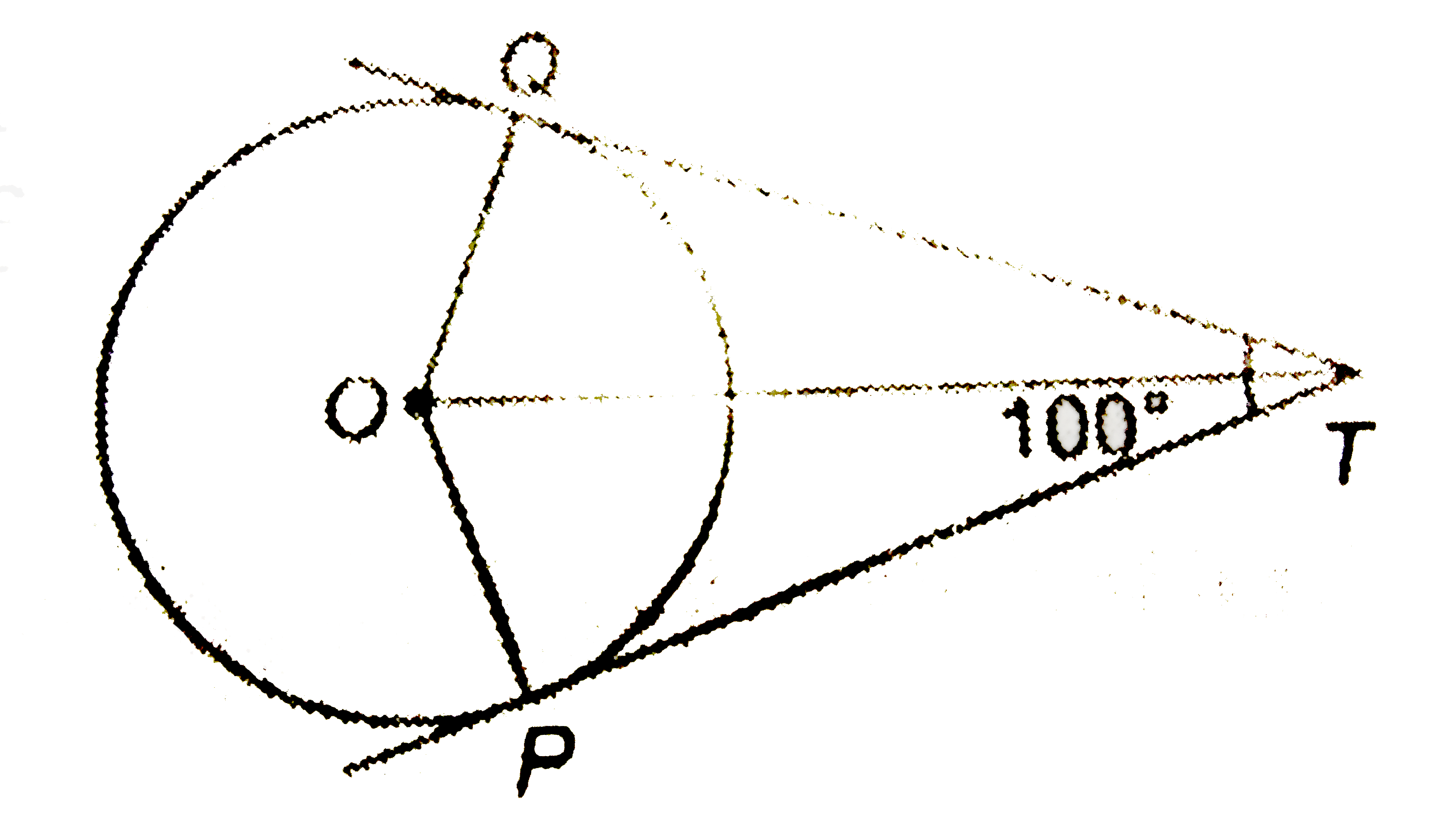
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View Solution
