Triangles on the same base and between the same parallels are equal in area.
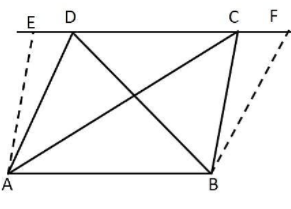
In ABFD
DF∣∣AB and BF∣∣AD
Thus, both pair of opposite sides are parallel.
Hence, ABFD id a parallelogram.
Similarly, we can prove that ABCE is a parallelogram with same base and between two parallels AB and EF.
ar(ABFD)=ar(ABCE)
In parallelogram ABFD,
Since diagonal of a parallelogram divides it into two congruent triangles.
△ABD≅△FBD
Area of congruent triangles are equal,
ar(ABD)=ar(FBD)
ar(ABFD)=2ar(ABD)
Similarly, we can prove that
ar(ABCE)=2ar(ABC)
Thus,
2ar(ABD)=2ar(ABC)
ar(ABD)=ar(ABC)
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 9.3
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.1
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 9.1
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Prove that Parallelograms on the same base and between the same parallels are equal in area.
View SolutionProve by vector method that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionUsing vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionIf a triangle and a parallelogram are on the same base and between the same parallels lines, then the area of the triangle is equal to half that of the parallelogram. GIVEN : A △ABCand∣∣gmBCDE on the same base BC and between the same parallels BCandAD. TO PROVE : ar(△ABC)=1/2 ar(∣∣gmBCDE) CONSTRUCTION : Draw AL ⊥ BC and DM⊥BC, produced at M.
View SolutionA triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
(a)1:1
(b) 1:2
(c) 2:1
(d) 1:3
View SolutionWhich of the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels: Figure (ii) Figure (iii) Figure Figure (ii) Figure (iii) Figure
View SolutionIf a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
View SolutionIn which of the following figures, you find two polygons on the same base and between the same parallels?
View SolutionIf a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is
View SolutionProve that two triangles having the same base and equal areas lie between the same parallels.
View Solution
