Two candidates contested from a constituency in an election. The winner secured 68% of the votes polled. If the difference between their votes was 23,040, find the voes secured by the winner.
The correct Answer is:43520
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Let the total votes be x:
- We denote the total number of votes polled in the election as x.
Hint: Define the total votes as a variable to simplify calculations.
2. Votes secured by the winner:
- The winner secured 68% of the total votes, which can be expressed as:
Votes secured by winner=68100×x=0.68x
Hint: Convert the percentage into a decimal to calculate the votes.
3. Votes secured by the loser:
- The loser secured the remaining votes, which is 32% of the total votes:
Votes secured by loser=32100×x=0.32x
Hint: Remember that the sum of the percentages of votes secured by both candidates should equal 100%.
4. Set up the equation for the difference in votes:
- According to the problem, the difference between the votes secured by the winner and the loser is 23,040. We can write this as:
0.68x−0.32x=23,040
Hint: Use the information about the difference in votes to form an equation.
5. Simplify the equation:
- Simplifying the left side gives:
0.36x=23,040
Hint: Combine like terms to simplify the equation.
6. Solve for x:
- To find x, divide both sides by 0.36:
x=23,0400.36
- Calculating this gives:
x=64,000
Hint: When dividing, ensure you maintain the decimal places correctly.
7. Calculate the votes secured by the winner:
- Now that we have the total votes, we can find the votes secured by the winner:
Votes secured by winner=0.68×64,000
- This calculation results in:
Votes secured by winner=43,520
Hint: Multiply the percentage of votes by the total to find the winner's votes.
Final Answer:
The votes secured by the winner is 43,520.
- We denote the total number of votes polled in the election as x.
- The winner secured 68% of the total votes, which can be expressed as:
Votes secured by winner=68100×x=0.68x
- The loser secured the remaining votes, which is 32% of the total votes:
Votes secured by loser=32100×x=0.32x
- According to the problem, the difference between the votes secured by the winner and the loser is 23,040. We can write this as:
0.68x−0.32x=23,040
- Simplifying the left side gives:
0.36x=23,040
- To find x, divide both sides by 0.36:
x=23,0400.36
- Calculating this gives:
x=64,000
- Now that we have the total votes, we can find the votes secured by the winner:
Votes secured by winner=0.68×64,000
- This calculation results in:
Votes secured by winner=43,520
The votes secured by the winner is 43,520.
Topper's Solved these Questions
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - EXERCISE 9.2
14 Videos
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE
26 Videos
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - CHALLENGE!
1 Videos
- PERCENTAGE BOOK - ICSECHAPTER - PERCENTAGE EXERCISE - EXERCISE 9C
26 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - TRY THIS
41 Videos
Similar Questions
In an election , two persons contested and the winner secured 58% of the votes polled. If the difference between their votes is 8480, find the votes secured by the winner.
View SolutionIn a student election, Rahul got 66 % of the votes polled. If he got 363 votes, find the total number of votes polled.
View Solution
Knowledge Check
In a multi-voting system, voters can vote for more than one candidate. Two candidate A and B are contesting the election. 100 voters voted for A. Fifty out of 250 voters voted for both the candidates. If each voter voted for at least one of the two candidates, then how many voters voted only for B?
A50B100C150D200
Two candidates A and B contested an election. The total votes polled were 9650. If A got 54% of the votes, find the number of votes received by each.
View SolutionAt an election between two candidates 53 votes were declared invalid. The winning candidate secures 58% of the valid votes and wins by 588 votes. Find the total number of votes polled.
View SolutionIn an election, there are two candidates A and B. The total number of voters is 60,000 and 80%of the total votes are polled. If 60% of the polled votes were cast in favour of A, how many votes were polled in favour of B?
View SolutionIn an election, two contestants A and B contested x% of the total voters voted for A and (x+20)% for B. If 20% of the voters did not vote, then x is
View SolutionMr. Gupta has a choice to invest in ten-rupee shares of two firms at 13rs or at 16rs. If the first firm pays 5% dividend and the second firm pays 6% dividend per annum, find :
(i) which firm is paying better
(ii) if Mr. Gupta invests equally in both the firms and the difference between the returns from them is 30rs, find how much, in all does he invest ?
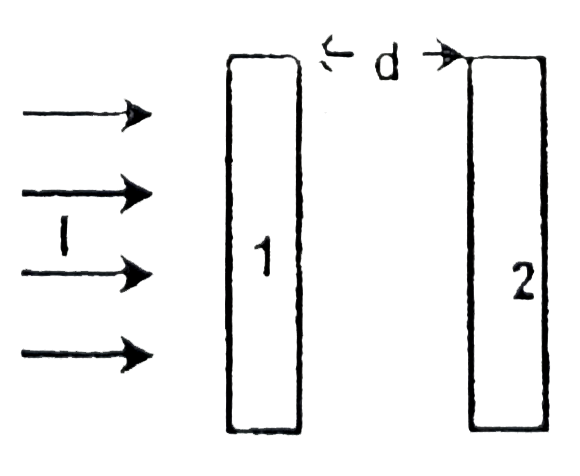
View SolutionTwo parallel large metal plates, each of area A are piaced at a distance d apart. Light of intensity I and wavelength λ falls on the plate 1 which is photosensitive. The efficiency of photoelectron emission is 100%. The photoelectrons are immediately swept away from plate 1 in such a way that the plate 2 remains neutral. Find the potential difference between the two plates at any time t, if plate 1 is neutral initially.
View SolutionIn an election the nuber oif candidates is one more than thenumber of members to be electeed. If a voter cn vote in 30 different weaqys, find the number of candidates (A voter has to vote for at least one candidate).
View Solution
