Question

Two circles are drawn through the points $(a,5a)\text{and}(4a,a)$ to touch the y-axis. Prove that they intersect at angle ${\tan }^{-1}\left(\frac{40}{9}\right).$

Options

A. `tan^(-1)(4//3)`
B. `tan^(-1)(40//9)`
C. `tan^(-1)(84//187)`
D. `pi//4`

Answer

B

Explanation

Equation of any circle through the given points is:
`(x-a) (x-4a) +(y-5a) (y-a) + lambda (4x+3y-19a) =0`, for some `lambda in R`.
As it touches the y-axis, putting `x =0` and comparing discriminant of resulting quadratic equation in x to 0, we get
`:. (-3a +(3lambda)/(2))^(2) = 9a^(2) - 19 lambda a`
`:. lambda = 0, (-40a)/(9)`.
`:.` The required circles are
`x^(2) + y^(2) - 5ax -6ay +9a^(2) =0`
`x^(2) +y^(2) - 5ax -6ay +9a^(2) -(40a)/(9) (4x +3y -19a) =0`
Hence centres are `((5a)/(2),3a)` and `((205a)/(18),(29a)/(3))`

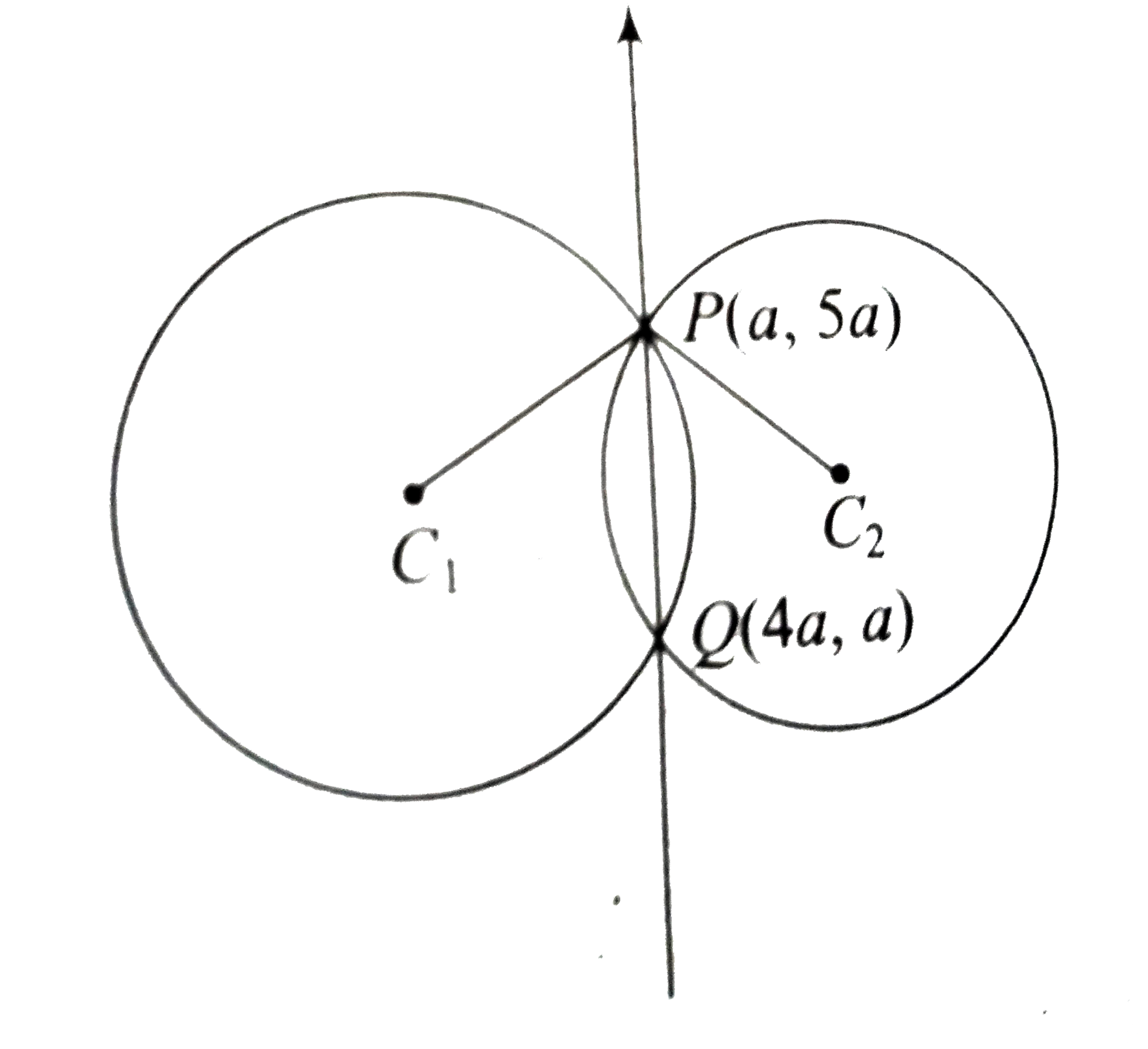
The centres of the given circles are:
`C_(1) ((205a)/(18),(29a)/(3))` and `C_(2) ((5a)/(2),3a)`
Now, the angle of intersection `theta` of these two circles is the angle between the radius vectors a the common point P to the two circles.
i.e., `/_C_(1)PC_(2) = theta`
and slope of `C_(2)P = (5a-3a)/(a-(5a)/(2)) = - (4)/(3)`
So, `tan theta = ((84)/(187)+(4)/(3))/(1-(84)/(187)xx(4)/(3)) =(252+748)/(561-336) =(40)/(9)`
`rArr theta = tan^(-1) ((40)/(9))`