Two circles are given such that one is completely lying inside the other without touching. Prove that the locus of the center of variable circle which touches the smaller circle from outside and the bigger circle from inside is an ellipse.Solution in Tamil
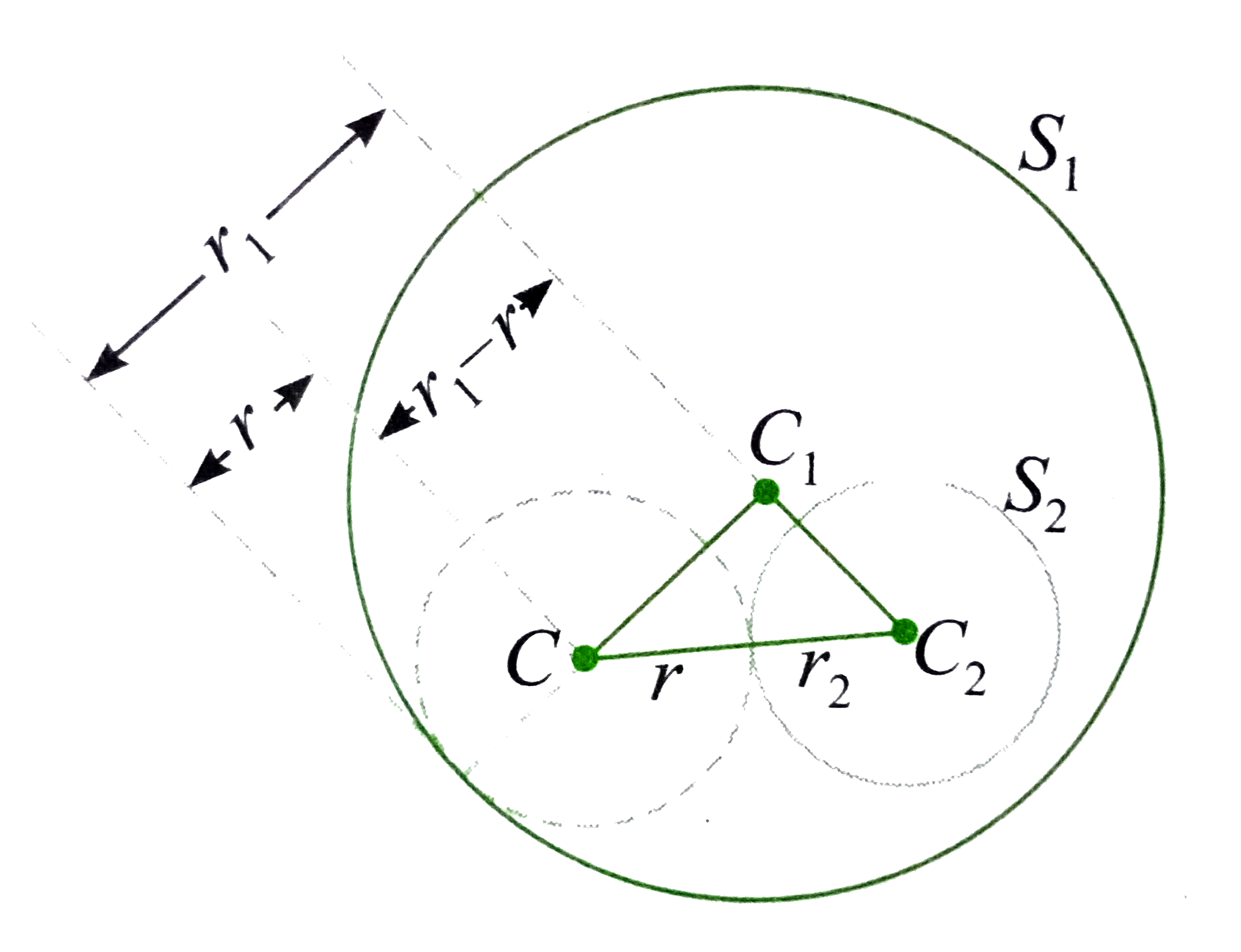
Let the circle S2 having centre at C2 and redius r2 lie completely insid the circle S1 having centre at C1 and radius r1
Variable circle S touches S1 intrnally and S2 externally. Centre C of circle S is variable point and its radius 'r' is also variable. From the figure CC2=r+r2andCC1=r1−r So, CC1+CC2=r1+r2 (constant) Thus, locus of C is ellips whose foci are at C1andC2
Similar Questions
ਸਿੱਧ ਕਰੋ ਕਿ ਦੋ ਸਮਕੇਂਦਰੀ ਚੱਕਰਾਂ ਵਿੱਚ ਵੱਡੇ ਚੱਕਰ ਦੀ ਜੀਵਾ ਜੋ ਛੋਟੇ ਚੱਕਰ ਨੂੰ ਸਪਰਸ਼ ਕਰਦੀ ਹੈ, ਸਪਰਸ਼ ਬਿੰਦੂ 'ਤੇ ਸਮਦੁਭਾਜਿਤ ਹੁੰਦੀ ਹੈ।
View SolutionTwo circles are given such that one is completely lying inside the other without touching. Prove that the locus of the center of variable circle which touches the smaller circle from outside and the bigger circle from inside is an ellipse.
View SolutionStatement 1 : The locus of the center of a variable circle touching two circle (x−1)2+(y−2)2=25 and (x−2)2+(y−1)2=16 is an ellipse. Statement 2 : If a circle S2=0 lies completely inside the circle S1=0 , then the locus of the center of a variable circle S=0 that touches both the circles is an ellipse.
View SolutionTwo circles are given such that they neither intersect nor touch. Then identify the locus of the center of variable circle which touches both the circles externally.
View SolutionTwo circles are given such that one is completely lying inside the other without touching. Prove that the locus of the center of variable circle which touches the smaller circle from outside and the bigger circle from inside is an ellipse.
View SolutionTwo circles are given such that they neither intersect nor touch. Then identify the locus of the center of variable circle which touches both the circles externally.
View SolutionProve that the locus of the center of the circle which touches the given circle externally and the given line is a parabola.
View SolutionStatement 1 : The locus of the center of a variable circle touching two circle (x−1)2+(y−2)2=25 and (x−2)2+(y−1)2=16 is an ellipse. Statement 2 : If a circle S2=0 lies completely inside the circle S1=0 , then the locus of the center of a variable circle S=0 that touches both the circles is an ellipse.
View Solution
