Two circles are inscribed and circumscribed about a square ABCD, ength of each side of the square is 32. P and Q are two points respectively on these circes, then [∑(QA)2−−∑(PA)2] is equal ot
The correct Answer is:1024
Topper's Solved these Questions
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - EXERCISE (CONCEPT-BASED ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
20 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - EXERCISE (LEVEL 1 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
53 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - SOLVED EXAMPLES (LEVEL 2 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
30 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B - ARCHITECTURE (ENTRANCE EXAMINATION PAPERS)
14 Videos
- COMPLEX NUMBERS BOOK - MCGROW HILL PUBLICATIONCHAPTER - COMPLEX NUMBERS EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPER
17 Videos
Similar Questions
Two circles are inscribed and circumscribed about a square ABCD, length of each side of the square is 32. P and Q are two points repectively on these circles, then σ(PA)2+σ(QA)2 equals __________ .
View SolutionTwo circles are inscribed are circumscribed about a square ABCD, length of each side of the square is 32. P and Q are two points repectively on these circles, then σ(PA)2+σ(QA)2 equals __________ .
View Solution
Knowledge Check
Two circles are such that one is inscribed in and the other is circumscribed about a square A1,A2,A3,A4, If the length of each side of the square is a and P, Q are two points respectively on these circles, then
∣∣ ∣∣4∑i=1(PAi)2−4∑i=1(AQi)2∣∣ ∣∣=Aa2/4Ba2/2Ca2D2a2The sum of the radii of the circles, which are respectively inscribed and circumscribed about a polygon of n sides, whose side length is a, is
A12atan(π2n)B12acot(π2n)C12cot(π3n)D12cot(π2n)In the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is 16cm2.
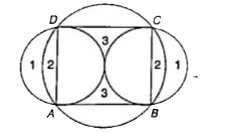
What is the area of region 2 ?A3(π−2)cm2B(π−3)cm2C(2π−3)cm2D4(π−2)cm2
ABCD is a square of side length 2. C1 is a circle inscribed in the square and C2 is a circle. circumscribing the square. P and Q are any two points on C1andC2 respectively. Also R is fixed point and L is a fixed line in the same plane. A circle C touches line L and circle C1 externally. S is a point which is equidistant from given point Rand fixed line L. Point R coincides with B.
PA2+PB2+PC2+PD2QA2+QB2+QC2+QD2=
View SolutionIn the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is 16cm2.
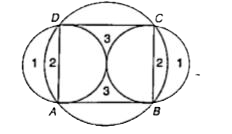
What is the area of region 1 ?
View SolutionIn the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is 16cm2.
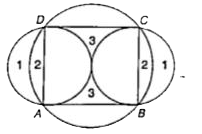
What is the area of region 3 ?
View SolutionIf twice the square on the diameter of a circle is equal to sum of the squares on the sides of the inscribed triangle ABC, then sin2A+sin2B+sin2C is equal to
View SolutionFour circles of equal radii are inscribed in a square of side 56 cm, touching each other such that each side of the square is tangent to two adjacent circles. The area of the square unoccupied by the circles is
View Solution
