Two circles drawn with centres A and B touch each other externally at C, O is a point on the tangent drawn at C, OD and OE are tangents drawn to the circles of centre A and B respectively. If then prove that Solution in Bengali
OC and OD are two tangents at the points C and D on the circle with centre at A form and ecternal point O.
Again, OC and OE are two tangents at the point C and E to the circle with centre B from an external point O.
[by theorem -41] ltbr Then from (1) and (2) we get,
Now in
We know that in
or,
Then [from (3) and (4) ]
Hence (Proved)

Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.120videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
09:02View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
07:17View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
06:21View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
05:22View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
02:26View SolutionTwo tangents are drawn from an external point A of the circle with centre at O which touches the circle at the points B and C. Prove that AO is the perpendicular bisector of BC.
03:05View SolutionProve that the internal bisector of the angle between two tangents drawn from an external point of a circle will pass through the centre of the circle.
03:10View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
 09:47View Solution
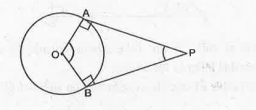
09:47View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
04:24View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
03:14View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
10:01View SolutionThe two central circles A and B are drawn which intersect each other at the point C. O is a point on the tangent drawn at point C and OD and OE touch the central circle A and B at points D and E respectively. angleCOD = 56^@, angleCOE = 40^@, angleACD = x^@ And angleBCE = y^@ Then prove that OD = OC = OE and xy = 8
01:55View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
04:55View SolutionIn figure, OD angle /_AOC Is the bisector of OE, /_BOC Is a bisector of and OD _|_ OE is. Show that A, O and B align.
05:14View SolutionProve tht the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
 05:49View Solution
05:49View Solution

