Two circles of radii $a a n d b$ touching each other externally, are inscribed in the area bounded by $y = \sqrt{1 - x^{2}}$ and the x-axis. If $b = \frac{1}{2},$ then $a$ is equal to $\frac{1}{4}$ (b) $\frac{1}{8}$ (c) $\frac{1}{2}$ (d) $\frac{1}{\sqrt{2}}$

A

$1 / 4$

B

$1 / 8$

C

$1 / 2$

D

$1 / \sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

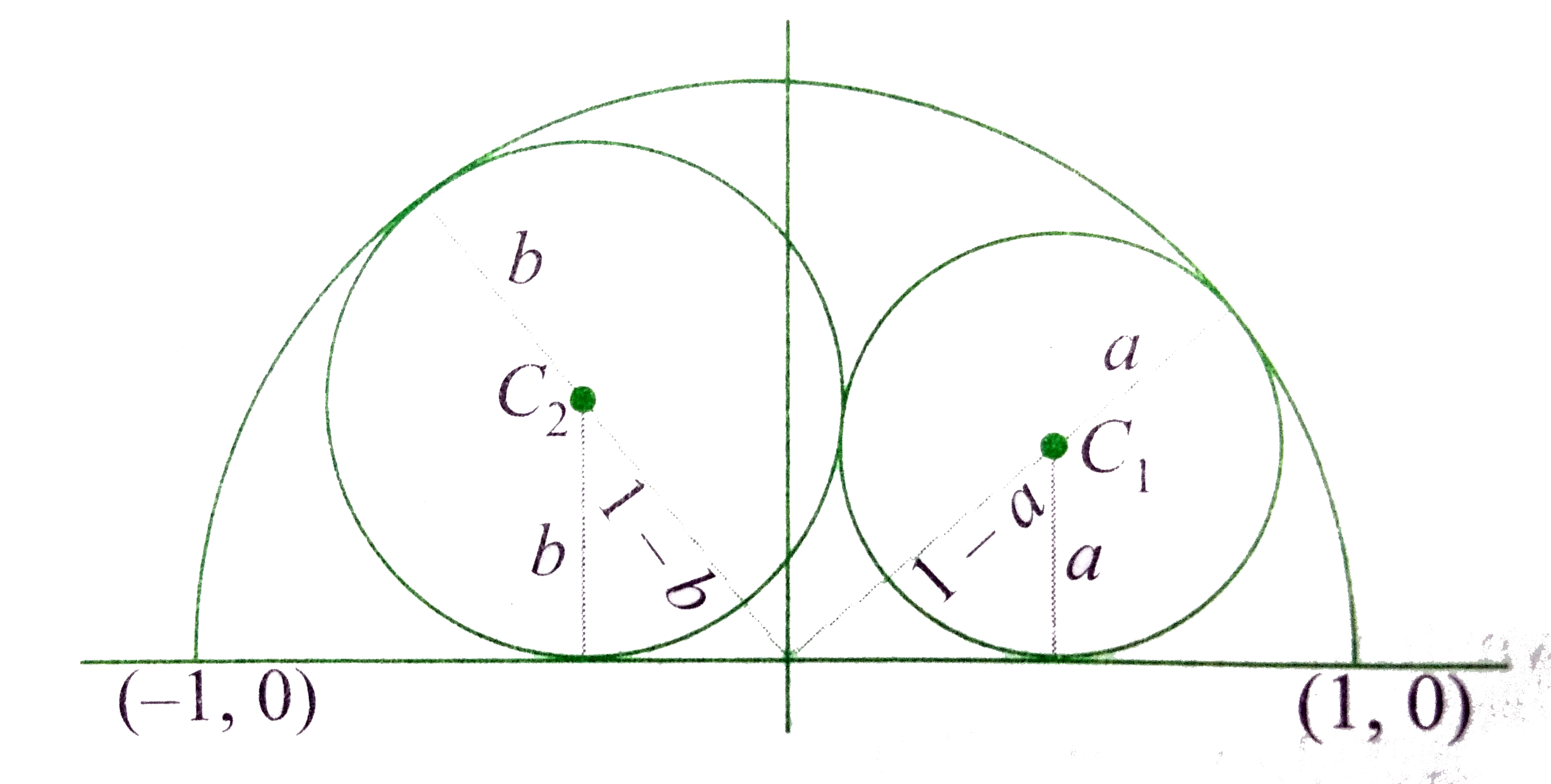
Let the centers of the circle be $C_{1}$ and $C_{2}$ .
Then $C_{1}$ is $(\sqrt{1 - 2 a}, a)$ and $C_{2}$ is $(\sqrt{1 - 2 b}, b)$ . Now,
$C_{1} C_{2} = a + b = a + \frac{1}{2}$
or $1 - 2 a + {(a - \frac{1}{2})}^{2} = {(a + \frac{1}{2})}^{2}$
or $a = \frac{1}{4}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by $y = {sin}^{- 1} x, x = \frac{1}{\sqrt{2}}$ and X-axis is
A $(\frac{1}{\sqrt{2}} + 1)$ sq units
B $(1 - \frac{1}{\sqrt{2}})$ sq units
C $\frac{π}{4 \sqrt{2}}$ sq units
D $(\frac{π}{4 \sqrt{2}} + \frac{1}{\sqrt{2}} - 1)$ sq units
Question 2 - Select One
The area bounded by the x-axis, the curve $y = f (x),$ and the lines $x = 1, x = b$ is equal to $\sqrt{b^{2} + 1} - \sqrt{2}$ for all $b > 1,$ then $f (x)$ is $\sqrt{x - 1}$ (b) $\sqrt{x + 1}$ $\sqrt{x^{2} + 1}$ (d) $\frac{x}{\sqrt{1 + x^{2}}}$
A $\sqrt{x - 1}$
B $\sqrt{x + 1}$
C $\sqrt{x^{2} + 1}$
D $\frac{x}{\sqrt{x^{2} + 1}}$
Question 3 - Select One
The area bounded by $y = \sqrt{1 - x^{2}}$ and $y = x^{3} - x$ is divided by y - axis in the ratio $λ : 1 (\forall λ > 1)$ , then $λ$ is equal to
A $\frac{π + 1}{π - 1}$
B $\frac{π}{π - 1}$
C $\frac{π + 1}{π}$
D $\frac{π + 2}{π - 2}$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile