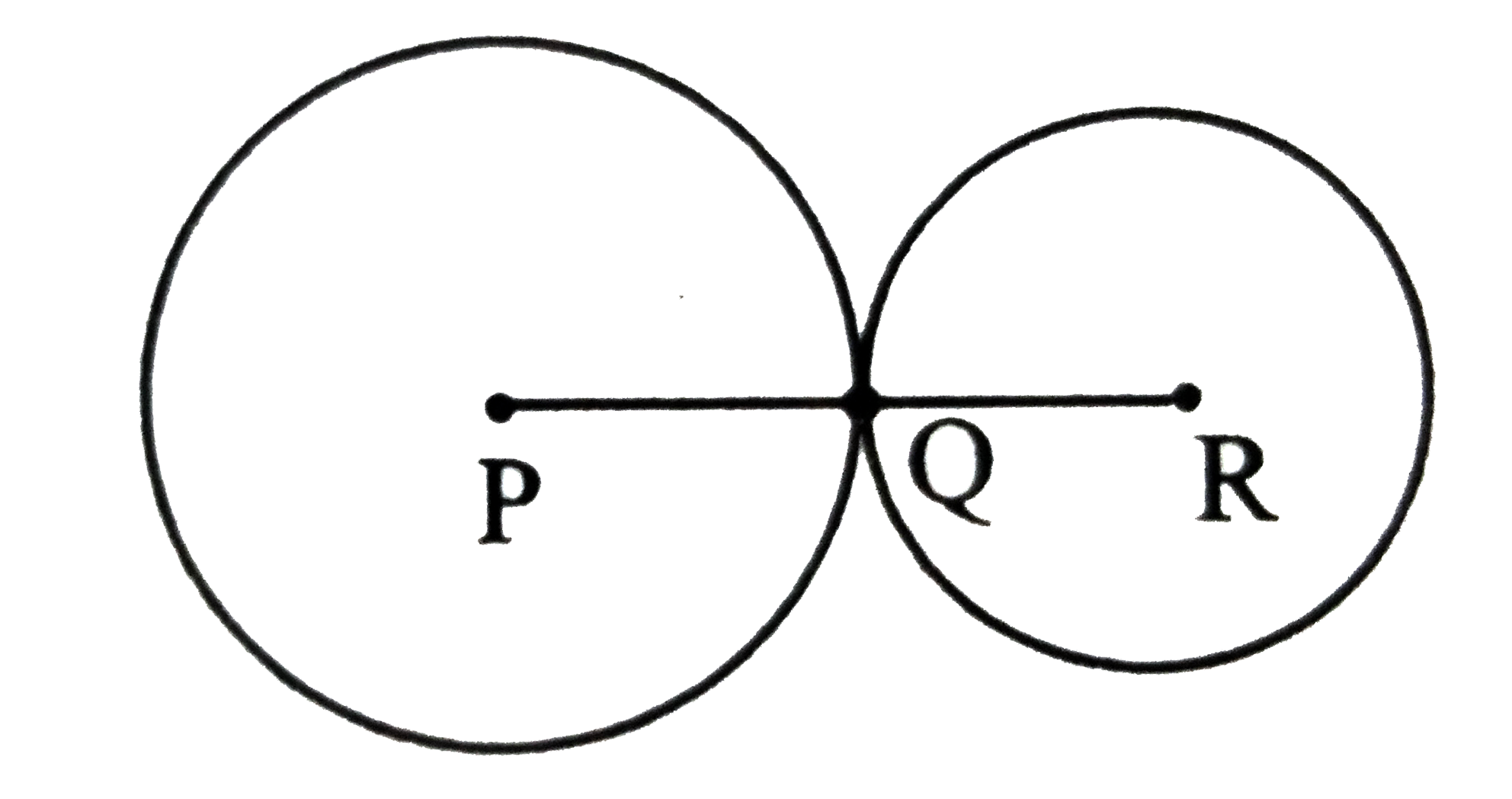
Two circles with radii 3 cm and 2.5 cm touch each other externally then find the distance between their centre.
Video Solution
Text Solution
Distance between their centres = Sum of their radii …( By theorem of touching circles )
=3+2.5
=5.5cm
Distance between their centres is 5.5 cm .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.3 (1 mark each)11videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.4 (1 mark each)9videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
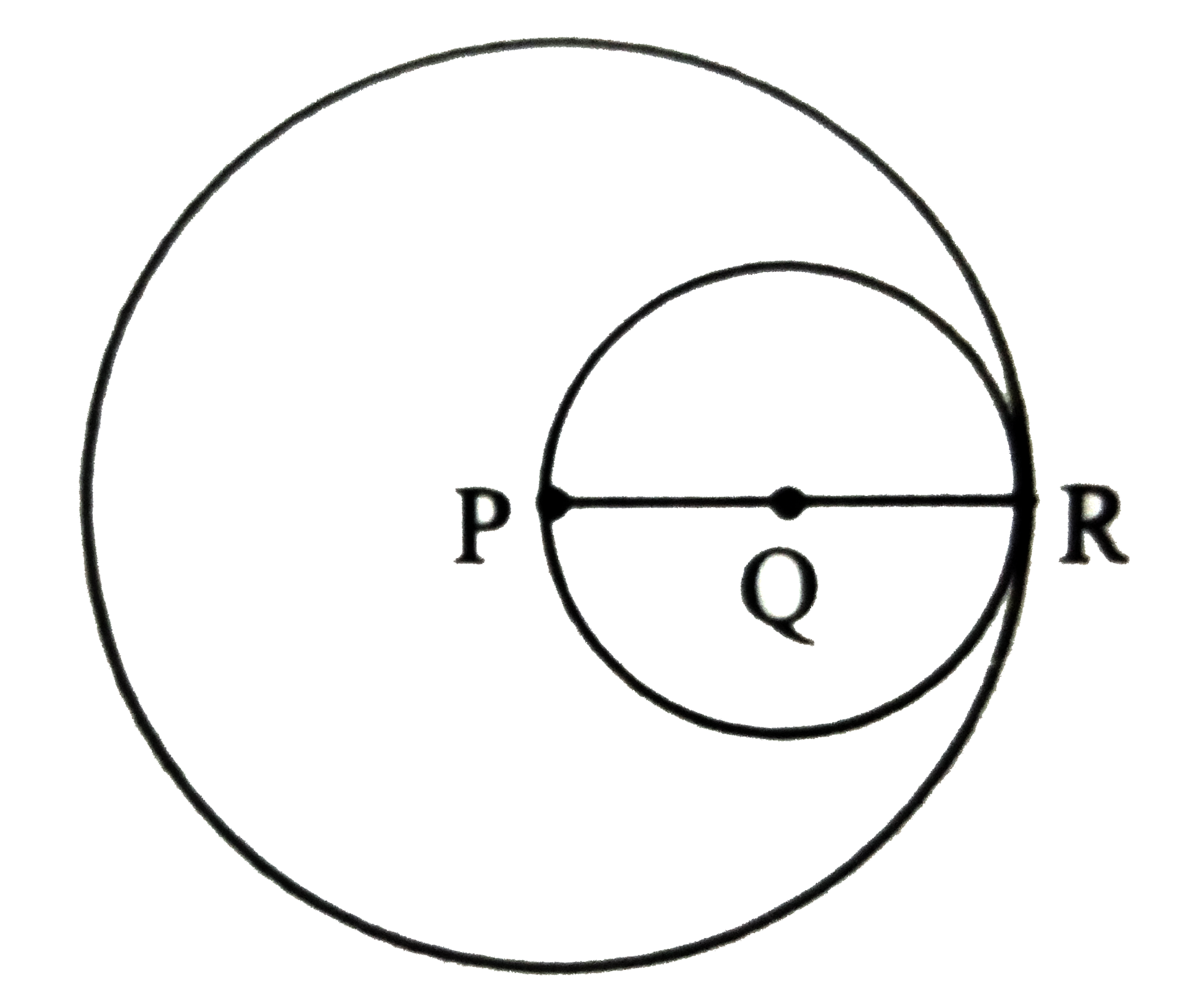
Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cmB12 cmC9 cmD8 cm - Question 2 - Select One
Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cmB12 cmC9 cmD8 cm
Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between thir centres.
View SolutionTwo circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between thir centres.
View SolutionTwo circles of radii 5.5cm and 4.2cm touch each other externally. Find the distance between their centres.
 View Solution
View SolutionTwo circles having radii 3.5cm and 4.8cm touch each other internally. Find the distance between their centres.
 View Solution
View SolutionIf two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres.
View SolutionIf two circles with radii 8 and 3 respectively touch externally, then find the distance between their centres.
View Solution

