Question

Two concentric ellipses are such that the foci of one are on the other
and their major axes are equal. Let $eande\text{'}$
be their eccentricities. Then.
the quadrilateral formed by joining the foci of the two ellipses is a
parallelogram
the angle $\theta$
between their axes is given by $\theta ={\cos }^{-1}\sqrt{\frac{1}{e^2}+\frac{1}{e^{\text{'}2}}=\frac{1}{e^2{e}^{\text{'}2}}}$

If $e^2+e^{\text{'}2}=1,$
then the angle between the axes
of the two ellipses is ${90}^0$

none of these

Options

A. the quadrilateral formed by joining the foci of the two ellipe is a parallelogram
B. the angle `theta` between their axes is give by `theta=cos^(-1)sqrt((1)/(e^(2))+(1)/(e'^(2))-(1)/(e^(2)e'^(2)))`
C. If `e^(2)+e'^(2)=1`, then the angle between th axes of the two ellipse is `90^(@)`
D. none of these

Explanation

Celeary, O is the midpoint of SS' and HH'

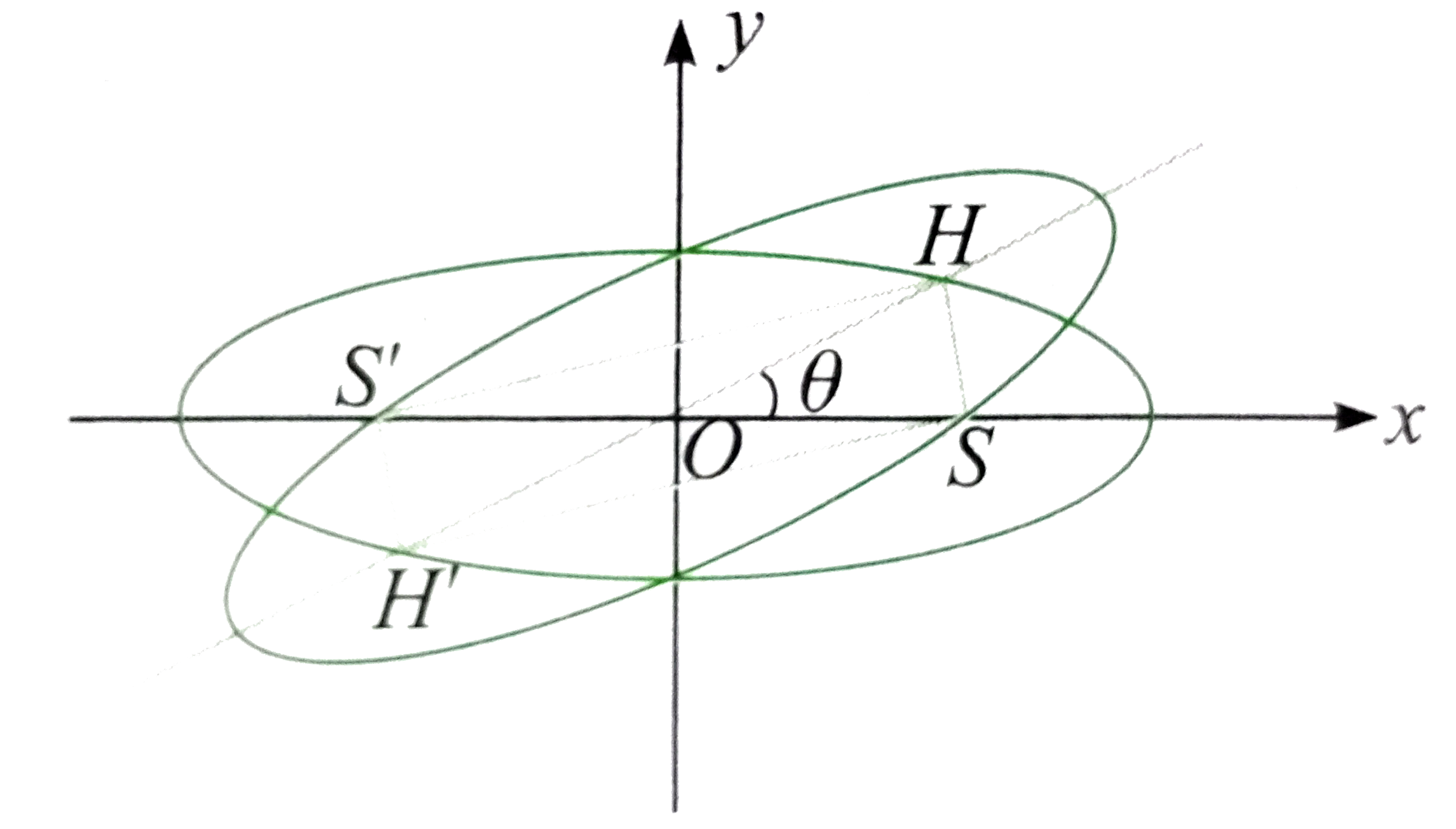
Therfore, the disagonals of quadrilateral HSH'S'' bisect each other. So it is a parallelogram.
The point H lies on
`(x^(2))/(a^(2))+(y^(2))/(b^(2))` (Suppose)
`:. (r^(2) cos^(2)theta)/(a^(2))+(r^(2)sin^(2) theta)/(b^(2))=1`
`e'^(2) cos^(2) theta+(e^(2)sin^(2) theta)/(1-e^(2))=1 " " [ :. b^(2)=a^(2)(1-e^(2))]`
or `e'^(2) cos^(2) theta -(e'^(2) cos^(2) theta)/(1-e^(2))=1-(e'^(2))/(1-e^(2))`
or `cos^(2)theta(1)/(e^(2))+(1)/(e'^(2))=(1)/(e^(2)e'^(2))`
or `theta= cos^(-1)sqrt((1)/(e^(2))+(1)/(e'^(2))-(1)/(e^(2)e'^(2)))`
For `theta=90^(@)`,
` (e^(2)+e'^(2))/(e^(2)e'^(2))=(1)/(e^(2)e'^(2))`
` or e^(2)+e'^(2)=1`