Two equal sides of an isosceles triangle are given by 7x−y+3=0 and x+y=3, and its third side passes through the point (1,−10). Find the equation of the third side.
Let AP and AQ be the internal and external bisectors of ∠ABC. Since AB=AC therefore AP⊥BCandAQ∣∣BCasAP⊥AQ, Thus BC passes through R(1,−10) and is parallel to AQ and RC' passes throug R(1,−10) and is parallel to internal bgisectors AP.
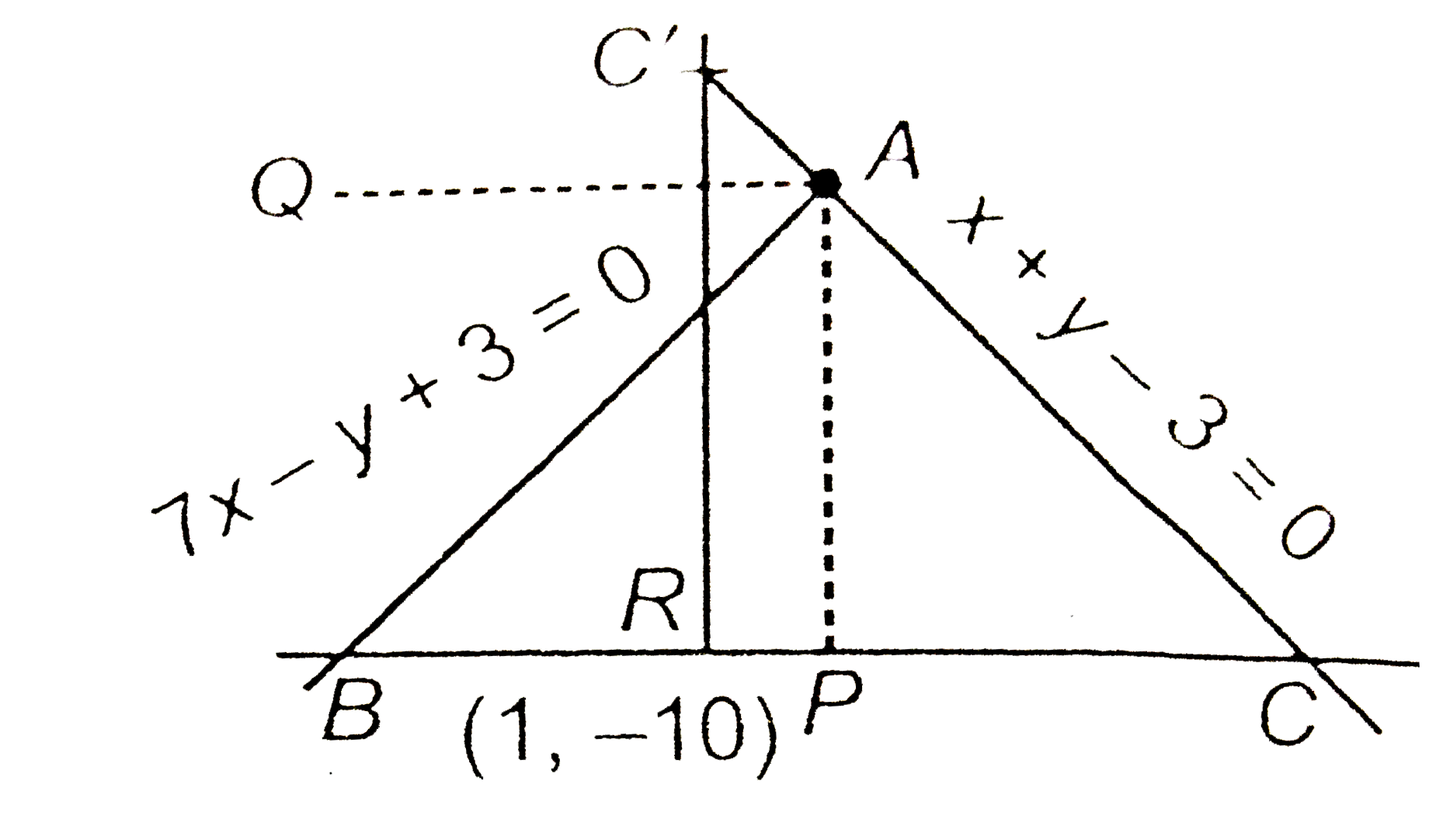
The equation of the two bisector of angle BAC are
7x−y+3√50=±x+y−3√2
⇒3x+y−3=0andx−3y+9=0. The line through (1,−10) parallel to 3x+y−3=0 is 3x+y−k=0 where 3−10−k=0,k=−7,
i.e., the strainght line through (1,−10) and parallel to 3x+y−3=0 is given by x−3y−31=0.
Hence the third side in its two positions (BC and B'C') have the equations 3x+y+7=0andx−3y−31=0.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - TRY YOURSELF23videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - ASSIGNMENT (SECTION A) (OBJECTIVE TYPE QUESTIONS) (ONLY ONE ANSWER)50videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason15videos
STATISTICS
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J10videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is
View SolutionTwo sides of an isosceles triangle are given by the equations 7x−y+3=0andx+y−3=0 and its third side passes through the point (1,−1). Determine the equation of the third side.
View Solution
Knowledge Check
- Question 1 - Select One
The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is
Ax - 3y = - 31Bx - 3y = 31Cx + 3y = 31Dx + 3y = - 31 - Question 2 - Select One
The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is
Ax−3y=−31Bx−3y=31Cx+3y=31Dx+3y=−31 - Question 3 - Select One
The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is
Ax−3y−7=0 or 3x+y−31=0Bx−3y−31=0 or 3x+y−7=0Cx−3y−31=0 or 3x+y+7=0DNone of these
Two equal sides of an isosceles triangle are 7x−y+3=0,x−y−3=0 and its third side passes through the point (1,0) the equation of the third side is (A) 3x+y+7=0 (B) x−3y+29=0 (C) 3x+y+3=0 (D) 3x+y−3=0
View SolutionTwo equal sides of an isosceles triangle are given by equations 7x−y+3=0 and x+y−3=0. It's third side passes through the point (1,−10). Determine the equation of the third side. (A)x−3y−31=0 (B) 3x+y+7=0 (C) Both (A), (B) (D) Neither (A), nor (B)
View SolutionEquation of two equal sides of a triangle are the lines 7x+3y−20=0 and 3x+7y−20=0 and the third side passes through the point (-3,, 3), then the equation of the third side can be -
View SolutionTwo equal sides of an isosceles triangle are given by the equations 7x−y+3=0 and x+y−3=0. The slope of the third side is
View SolutionThe equation of the side AB and AC of a triangle ABC are 3x+4y+9 and 4x−3y+16=0 respectively. The third side passes through the point D(5,2) such that BD:DC=4:5. Find the equation of the third side.
View Solution

