Two houses stand just on the opposite sides of a road of a village. A ladder that stands against the wall of the first house is at a distance of 6 metres from the house and makes an angle of 30∘ with the horizontal line.But if the ladder stands against the wall of the second house keeping its foot at the same point, it makes an angle of 60∘ with the horizontal line.
(a) Find the length of the ladder.
(b) Calculate the distance of the foot of the ladder from the foot of the wall of the second house.
(c) Find the width of the road.
Find the height where the top of the ladder is fixed against the wall of the second house. Solution in Bengali
Let AB and CD be two houses so that BD is the width of the road. The ladder PQ makes an angle of 30∘when it is against the first house AB and the same ladder PR madkes an angle of 60∘ when it is against the second house CD.
∴∠BPQ=30∘and∠DPR=60∘
As per question, BP = 6 metres
Now, from the right-angled triangle BPQ we get,
cos30∘=BPPQ [ by definition ]
or, √32=6PQ or,√3PQ=12 or, PQ=12√3=4√3.√3√3=4√3
Hence the length of the ladder =4√3 metres.
Again. from the right-angled triangle DPR we get,
cos60∘=PDPR [ by definition ]
or, 12=PDPQ[∵ PR = PQ ]
or, 12=PD4√3 or, 2PD=4√3 or,PD=4√32or,PD=2√3.
∴ BD=BP+PD=(6+2√3)m.
Also, from the right-angled triangle PDR we get,
sin60∘=DRPR [ by definition ]
or, √32=DRPQ[∵PR=PQ]
or, √32=DR4√3 or,2DR=12 or,DR=122=6
Hence the ladder is fixed against the wall of the second houe at a height of 6 metres above the ground.
Hence (a) the length of the ladder is 4√3 m.
(b) the distance of the foot of the ladder from the foot of the wall of the second house is 2√3m.
(c) the width of the road is 2(3+√3) m.
(d) the height where the top of the ladder is fixed against the wall of the second house is 6 m.

Topper's Solved these Questions
- APPLICATION OF TRIGONOMETRIC RATIOS: HEIGHTS AND DISTANCESBOOK - CALCUTTA BOOK HOUSECHAPTER - APPLICATION OF TRIGONOMETRIC RATIOS: HEIGHTS AND DISTANCESEXERCISE - EXERCISE (Multiple choice question (MCQ) :
4 Videos
- APPLICATION OF TRIGONOMETRIC RATIOS: HEIGHTS AND DISTANCESBOOK - CALCUTTA BOOK HOUSECHAPTER - APPLICATION OF TRIGONOMETRIC RATIOS: HEIGHTS AND DISTANCESEXERCISE - EXERCISE (Write true or fals :)
2 Videos
- APPLICATION OF TRIGONOMETRIC RATIOS: HEIGHTS AND DISTANCESBOOK - CALCUTTA BOOK HOUSECHAPTER - APPLICATION OF TRIGONOMETRIC RATIOS: HEIGHTS AND DISTANCESEXERCISE - Example 2. Shor-answer-type question (SA) :
6 Videos
- COMPOUND INTERESTBOOK - CALCUTTA BOOK HOUSECHAPTER - COMPOUND INTERESTEXERCISE - SHORT ANSWERS TYPE QUESTIONS
10 Videos
Similar Questions
A tower stands vertically on the ground. From a point on the ground.which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45∘. Then the height of the tower is
View SolutionThe line of sight is the straight line drawn from the eye of an observer to the point where the object is viewed by the observer.
View SolutionIf the angle of elevation of a kite is 60∘ and the length of thread is 20√3 meters, calculate the height of kite above the ground.
View SolutionMr. Patul deposited Rs. 15000 in a bank. If the rate of annual compound interest be 12% then find the amount after 9 months when interests is compounded at the interval of 3 months.
View SolutionProblems in which a ladder is leaning against a wall making some angle; ex-1 The ladder is leaning against the wall makes an angle of 600 with the ground. If the length of the ladder is 19m , find the length of the foot of the ladder from the wall.
View Solutionकिसी घर की एक दीवार पर एक सीढ़ी इस प्रकार खड़ी है कि इसका ऊपरी सिरा दीवार के शिखर को छू रहा है | सीढ़ी का पाद दीवार से 2 मीटर की दूरी पर है | यदि सीढ़ी जमीन की सतह के साथ 60∘का कोण बना रही है, तो दीवार की ऊँचाई ज्ञात करो |
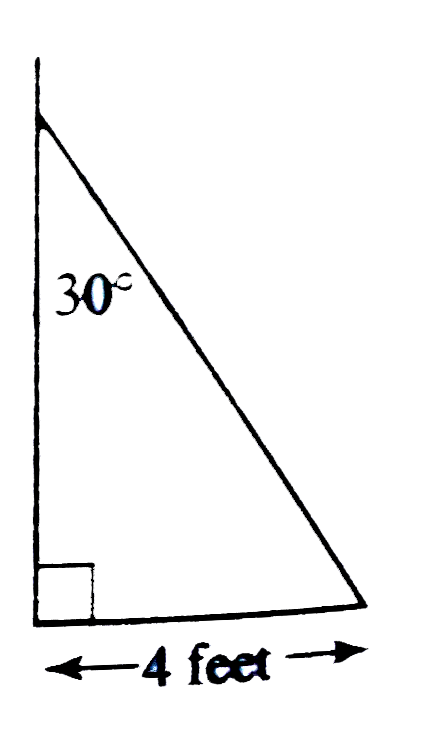
View SolutionA foot of a ladder leaning against the wall of a house is 4 feet from the base of the wall. If the ladder makes a 30∘ angle with the wall, what is the length, in feet, of the ladder ?
View SolutionThe angle of elevation of ladder learing against a house is 58∘ and the toot of the ladder is 9.6 m from the house. Then the length of the ladder is :
View SolutionThe angle of elevation of a ladder leaning against a wall is 60∘ and the foot of the ladder is 4.6 metre away from the wall . The length of the ladder is
View SolutionA ladder leaning against a wall makes an angle of 60∘ with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
View Solutionআমাদের পাড়ায় রাস্তার দু-পাশে পরস্পর বিপরীত দিকে দুটি বাড়ি আছে । প্রথম বাড়ির দেয়ালের গোড়া থেকে 6 মিটার দূরে একটি মই-এর গোড়া রেখে যদি মইটিকে দেয়ালে ঠেকানো যায়, তবে তা অনুভূমিক রেখার সঙ্গে 30∘ কোণ উৎপন্ন করে । কিন্তু মইটিকে যদি একই জায়গায় রেখে দ্বিতীয় বাড়ির দেয়ালে লাগানো যায়, তাহলে অনুভূমিক রেখার সঙ্গে 60∘ কোণ উৎপন্ন করে । মইটির দৈর্ঘ্য নির্ণয় করো ।
View SolutionA ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
View SolutionA ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2m away from the wall and the ladder is making an angle of 60∘ with the level of the ground. Determine the height of the wall.
View Solutionएक सीढ़ी एक मकान की दीवार के सहारे खड़ी है। उसके ऊपर का सिरा भूमि से 15 मी ऊँची मकान की खिड़की से सटा हुआ है। यदि दीवार के 7.5 मी ऊँचे बिन्दु से क्षैतिज रेखा खींची जाए, तो वह सीढ़ी की लम्बाई को निम्नलिखित अनुपात में विभाजित करेगी।
View SolutionA ladder rests against a wall making an angle α with the horizontal. The foot of the ladder is pulled away from the wall through a distance ‘a’ so that it slides a distance ‘b’ down the wall making an angle beta with the horizontal then the value of ab is
View Solution
