Two integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.Solution in Tamil
Since x and y each can take values from 0 to 10, so the total number of ways of selecting x and y is 11×11=121. Now, |x−y|>5
implies x−y<−5orx−y>5
When x−y>5, we have following cases:
Values of xValue of yNumber of cases60170, 1280, 1, 2390, 1, 2, 34100, 1, 2, 3, 45Total number of cases15
Similarly, we have 15 cases for x−y<−5. There are 30 pairs of values of x and y satisfying these two inequalities. So, favorable number of ways is 30. Hence, required probability is 30/121.
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Solved Example
1 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
24 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year
25 Videos
Similar Questions
There are two bags each containing 10 books all having different titles but of the same size. A student draws out books from the first bag as well as from the second bag. Find the probability that the different between the books drawn from the two bags does not exceed 2.
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
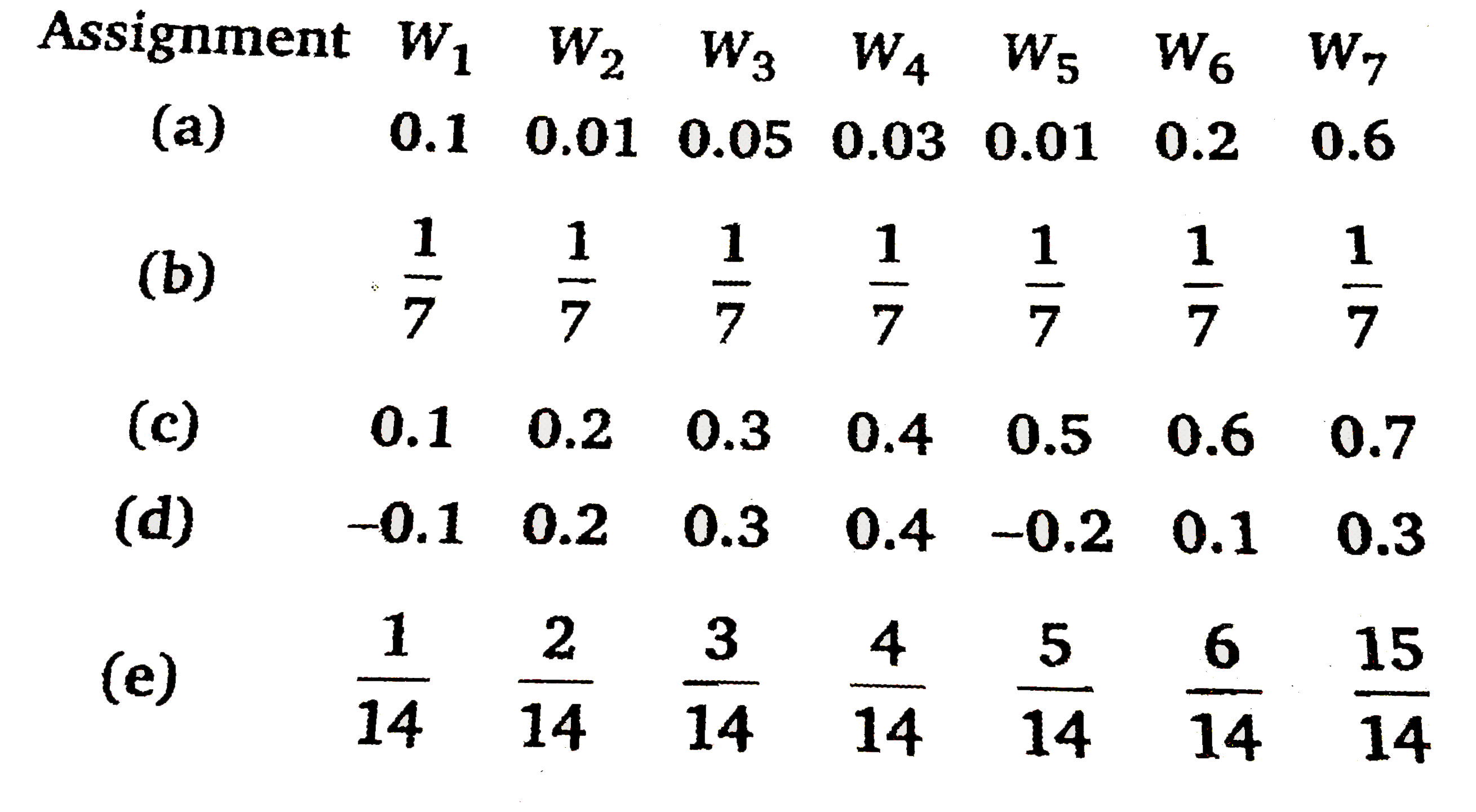
View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
View SolutionA signal which can be green or red with probability 45and15 respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is 34 If the signal received at station B is green, then the probability that the original signal was green is (a) 35 (b) 67 (c) 2023 (d) 920
View SolutionTwo integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.
View SolutionTwo integers x and y are chosen (with replacement) at random from {x:0<=x<=10,x is an integer).If the probability for |x-y|<=5 is p, then the value of (121p)/(13) is
View SolutionTwo non-negative integers x and y are chosen at random with replacement. The probability that x2+y2 is divisible by 10, is
View Solutionसमुच्चय [0,1,2…….,10] में से दो पूर्णांकों x और y,प्रतिस्थापन सहित चुने जाते हैं । |x−y|>5 के होने कि प्रायिकता है
View SolutionTwo integers x and y are chosen with replacement out of the set {0, 1, 2, . . . 10}. The probability that |x - y| doesn't exceed 5 is
View SolutionTwo distinct integers x and y are chosen, without replacement, at random from the set {x,y∣0≤x≤10,0≤y≤10 , x and y are in integers} the probability that |x−y|≤5 is :
View SolutionTwo integers x and y are chosen with replacement out of the set {0,1,2,3,….10} Then the probability that |x-y|>5 is
View SolutionTwo integers x and y are chosen (with replacement) out of the set {0,1,2,…10}. Find the probability that |x−y|≤5.
View SolutionTwo integers x and y are chosen with replacement out of the set {0, 1, 2, 3, ... 10). Then the probability that |x - y । > 5 is:
View SolutionTwo integers xandy are chosen with replacement out of the set {0,1,,2,3,.....10}. Then find the probability that |x−y|>5.
View SolutionTwo integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.
View SolutionTwo integers x and y are chosen one by one with replacement at random from the set {x =0 ≤ x ≤ 10 and x is an integer}. Find the probability that |x−y|≤5.
View Solution
