Two integers xandy are chosen with replacement out of the set {0,1,,2,3,.....10}. Then find the probability that |x−y|>5.Solution in Bengali
Since x and y each can take values from 0 to 10, so the total number of ways of selecting x and y is 11×11=121. Now, |x−y|>5
implies x−y<−5orx−y>5
When x−y>5, we have following cases:
Values of xValue of yNumber of cases60170, 1280, 1, 2390, 1, 2, 34100, 1, 2, 3, 45Total number of cases15
Similarly, we have 15 cases for x−y<−5. There are 30 pairs of values of x and y satisfying these two inequalities. So, favorable number of ways is 30. Hence, required probability is 30/121.
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Solved Example
9 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
When a fair dice is rolled, the number that comes up top is a number between one to six. Assuming we roll the dice once, to check the possibility of three coming up.
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
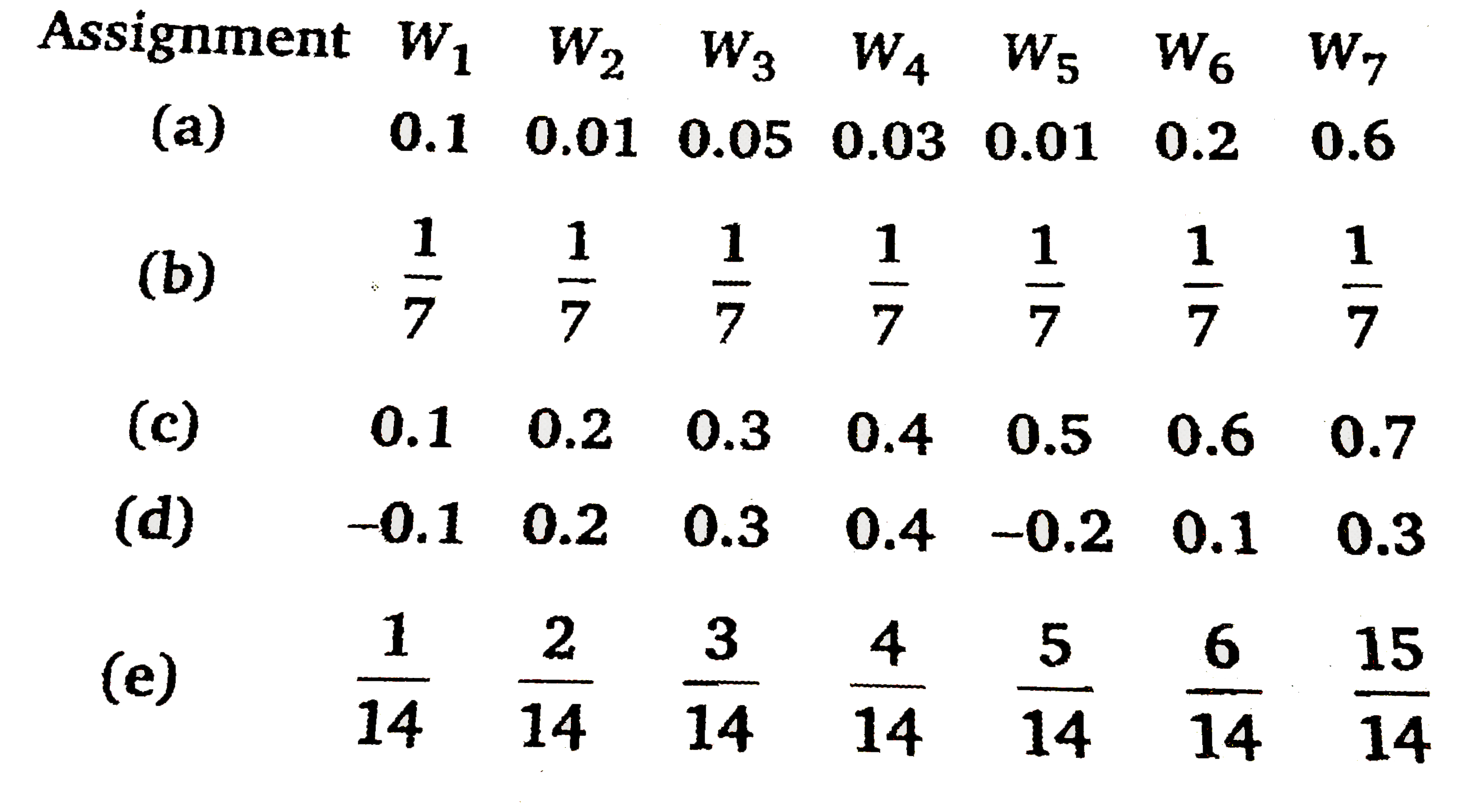
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionTwo integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.
View SolutionTwo integers x and y are chosen (with replacement) at random from {x:0<=x<=10,x is an integer).If the probability for |x-y|<=5 is p, then the value of (121p)/(13) is
View SolutionTwo non-negative integers x and y are chosen at random with replacement. The probability that x2+y2 is divisible by 10, is
View Solutionसमुच्चय [0,1,2…….,10] में से दो पूर्णांकों x और y,प्रतिस्थापन सहित चुने जाते हैं । |x−y|>5 के होने कि प्रायिकता है
View SolutionTwo integers x and y are chosen with replacement out of the set {0, 1, 2, . . . 10}. The probability that |x - y| doesn't exceed 5 is
View SolutionTwo distinct integers x and y are chosen, without replacement, at random from the set {x,y∣0≤x≤10,0≤y≤10 , x and y are in integers} the probability that |x−y|≤5 is :
View SolutionTwo integers x and y are chosen with replacement out of the set {0,1,2,3,….10} Then the probability that |x-y|>5 is
View SolutionTwo integers x and y are chosen (with replacement) out of the set {0,1,2,…10}. Find the probability that |x−y|≤5.
View SolutionTwo integers x and y are chosen with replacement out of the set {0, 1, 2, 3, ... 10). Then the probability that |x - y । > 5 is:
View SolutionTwo integers xandy are chosen with replacement out of the set {0,1,,2,3,.....10}. Then find the probability that |x−y|>5.
View SolutionTwo integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.
View SolutionTwo integers x and y are chosen one by one with replacement at random from the set {x =0 ≤ x ≤ 10 and x is an integer}. Find the probability that |x−y|≤5.
View Solution
