Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find E(X).
The correct Answer is:N/a
Number of ways of selecting any two positive integers from first six integers without repeating are 6×5=30.
Therefore the values of random variable X can be 2,3,4,5 or 6.
P(X=2)=P (selecting a number 2 and the other ess than 2)
=P(1,2),(2,1)
230=115
P(X=3)=P (selecting a number 3 and the other less than 3)
=P[(1,3),(2,3),(3,1) and (3,2)]
=430=215
P(X=4)=P (selecting a number 4 and the other less
P⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣142434414243⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦
=630=315
P(X=5)=P (selecting a number 5 and the other less than 5)
=P[(1,5),(2,5),(3,5),(4,5),(5,1),
(5,2),(5,3),(5,4)]
=830=415
P(X=6)=P (selecting a number 6 and the other less than 6)
=P[(1,6),(2,6),(3,6),(4,6),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5)]
=1030=13
Therefore required proibability distribution is
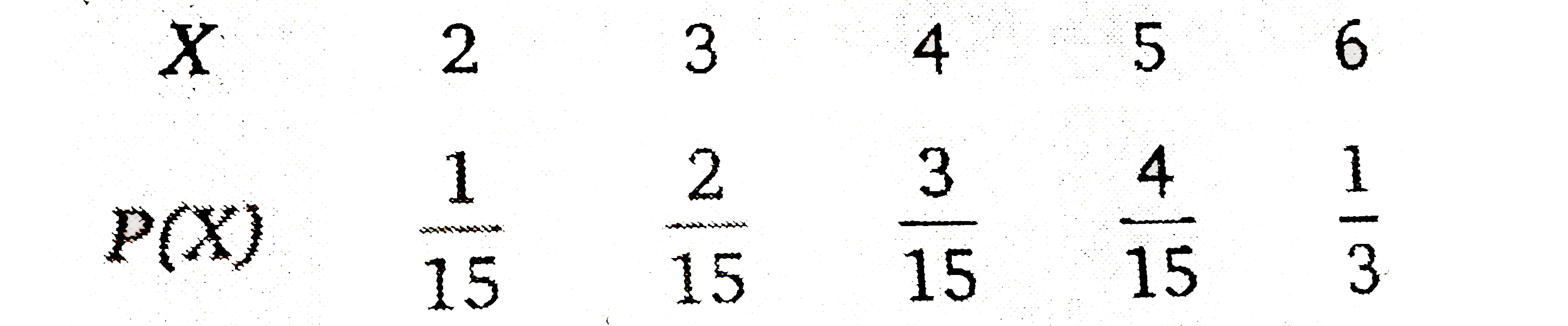
∴ Expectation of X=E(X)=∑XP(X)
2×115+3×215+4x315+5×415+6×13
=2+6+12+20+3015=7015=143
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Exercise 13.515videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise19videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Exercise 13.314videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise19videos
RELATIONS AND FUNCTIONS
Similar Questions
Two numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of X. Find the mean and variance of this distribution.
View SolutionTwo numbers are selected at random(without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X
View Solution
Knowledge Check
- Question 1 - Select One
What time taken by sum of rs.7000 to become rs.10500 at the rate of 5% per annum?
Aa. 8yearsBb. 10yearsCc. 5yearsDd. 15years - Question 2 - Select One
Three numbers are selected at random without replacement from the set of numbers {1, 2, 3, … n}. The conditional probability that the 3rd number lies between the 1st two. If the 1st number is known to be smaller than the 2nd, is
A13B23C56D712
three numbers are selected at random (without replacement) from first six positive integers. Let X denote the largest of the three numbers obtained. the probability distribution of X. Also, find the mean
View SolutionTwo numbers are selected at random (without replacement) from positive integers 2,3,4,5,6, and 7 . Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X .
View SolutionTwo numbers are selected are random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X.
View SolutionTwo numbers are selected at random (without replacement) from first 7 natural numbers. If X denotes the smaller of the two numbers obtained, find the probability distribution of X. Also, find mean of the distribution.
View SolutionTwo numbers are selected at random from 1,2,3,......100 without replacement. Find the probability that the minimum of the two numbers is less than 70.
1) 301330
2) 2933
3) 299330
4) 31330View SolutionA fair coin is tossed 3 times. Let X be the number of heads obtained. Find E(X) and V(X).
View Solution

