Two points O(0,0) and A(3,√3) with another point P form an equilateral triangle. Find the coordinates of P.
To find the coordinates of point P that, along with points O(0,0) and A(3,√3), forms an equilateral triangle, we can follow these steps:
Step 1: Calculate the length of side OA
Using the distance formula:
D=√(x2−x1)2+(y2−y1)2
For points O(0,0) and A(3,√3):
OA=√(3−0)2+(√3−0)2=√32+(√3)2=√9+3=√12=2√3
Step 2: Set up the equations for distances OP and AP
Let the coordinates of point P be (x,y). The distances OP and AP can be expressed as:
OP=√x2+y2
AP=√(x−3)2+(y−√3)2
Step 3: Set up the equations based on the property of equilateral triangles
Since OA=OP=AP, we can equate:
OA2=OP2andOA2=AP2
Step 4: Equate OA2 and OP2
(2√3)2=x2+y2
12=x2+y2(1)
Step 5: Equate OA2 and AP2
(2√3)2=(x−3)2+(y−√3)2
12=(x−3)2+(y−√3)2
Expanding the right side:
12=(x2−6x+9)+(y2−2√3y+3)
12=x2+y2−6x−2√3y+12
Substituting x2+y2 from equation (1):
12=12−6x−2√3y+12
This simplifies to:
0=−6x−2√3y
Dividing through by -2:
3x+√3y=0(2)
Step 6: Solve equations (1) and (2)
From equation (2):
√3y=−3x⇒y=−3√3x=−√3x
Substituting y in equation (1):
x2+(−√3x)2=12
x2+3x2=12
4x2=12⇒x2=3⇒x=√3 or x=−√3
Step 7: Find corresponding y values
1. If x=√3:
y=−√3(√3)=−3
So one point is P(√3,−3).
2. If x=−√3:
y=−√3(−√3)=3
So the other point is P(−√3,3).
Final Coordinates of Point P
The coordinates of point P are:
P(√3,−3)andP(−√3,3)
Using the distance formula:
D=√(x2−x1)2+(y2−y1)2
For points O(0,0) and A(3,√3):
OA=√(3−0)2+(√3−0)2=√32+(√3)2=√9+3=√12=2√3
Let the coordinates of point P be (x,y). The distances OP and AP can be expressed as:
OP=√x2+y2
AP=√(x−3)2+(y−√3)2
Since OA=OP=AP, we can equate:
OA2=OP2andOA2=AP2
(2√3)2=x2+y2
12=x2+y2(1)
(2√3)2=(x−3)2+(y−√3)2
12=(x−3)2+(y−√3)2
Expanding the right side:
12=(x2−6x+9)+(y2−2√3y+3)
12=x2+y2−6x−2√3y+12
Substituting x2+y2 from equation (1):
12=12−6x−2√3y+12
This simplifies to:
0=−6x−2√3y
Dividing through by -2:
3x+√3y=0(2)
From equation (2):
√3y=−3x⇒y=−3√3x=−√3x
Substituting y in equation (1):
x2+(−√3x)2=12
x2+3x2=12
4x2=12⇒x2=3⇒x=√3 or x=−√3
1. If x=√3:
y=−√3(√3)=−3
So one point is P(√3,−3).
y=−√3(−√3)=3
So the other point is P(−√3,3).
The coordinates of point P are:
P(√3,−3)andP(−√3,3)
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.13
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.14
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.11
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If (-4, 0) and (4,0) are two vertices of an equilateral triangle, find the coordinates of its third vertex.
View SolutionIf the point (0,0),(2,2√3), and (p,q) are the vertices of an equilateral triangle, then (p ,q) is
View SolutionShow that the points
(2,4),(2,6)(2+√3,5) form an equilateral triangle.
View SolutionIf three points (0, 0), (3, √3) and (3, λ) form an equilateral triangle, then λ= (a) 2 (b) −3 (c) −4 (d) None of these
View SolutionShow that the points (a,a),(−a,−a) and (−√3a,√3a) are the vertices of an equilateral triangle. Also, find its area.
View SolutionProve that the points A(1,1),B(−1,−1)andC(√3,−√3) are the vertices of an equilateral triangle.
View SolutionIf (-4,3) and (4,3) are two vertices of an equilateral triangle, then find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
View SolutionIn the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
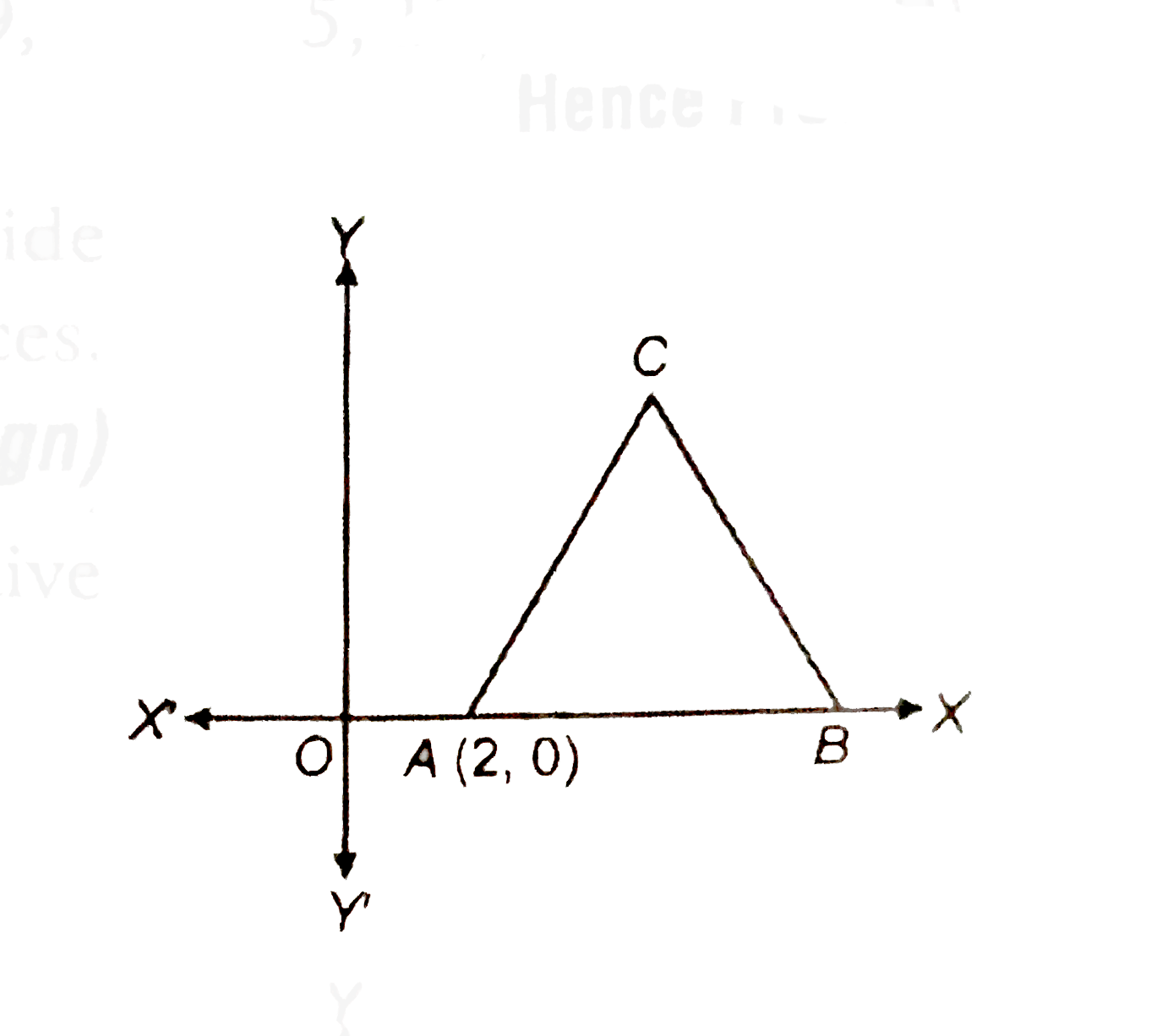
View SolutionIf O is the origin, OP=3 with direction ratios −1,2,and−2, then find the coordinates of P.
View SolutionShow that the points P(7,3) , Q ( 6,3+√3) and R (5,3) from an equilateral triangles.
View Solution
