Two probability distributionof the discrete random variable X and Y are given below.

Prove that E(Y2)=2E(X).
Video Solution
Text Solution
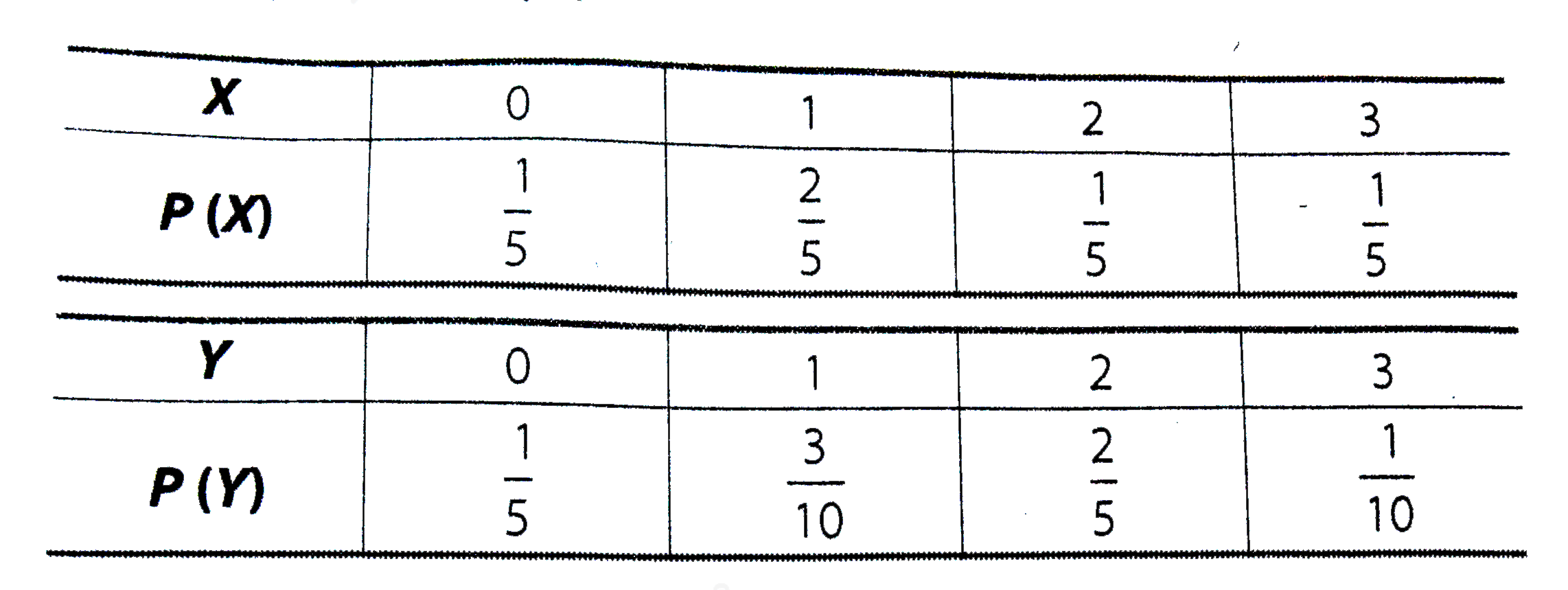
Since, we have to prove that, E(Y2)=2E(X) ltbr gtE(X)=ΣXP(X)
=0⋅15+1⋅25+3⋅15=75
⇒2E(X)=145
E(Y2)=ΣY2P(Y)
=0⋅15+1⋅310+4⋅25+9⋅110
=310+85+910=2810=145
⇒E(Y2)=145
From Eqs. (i) and (ii),
E(Y2)=2E(X) Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The probability distribution of a discrete random variable X is given below
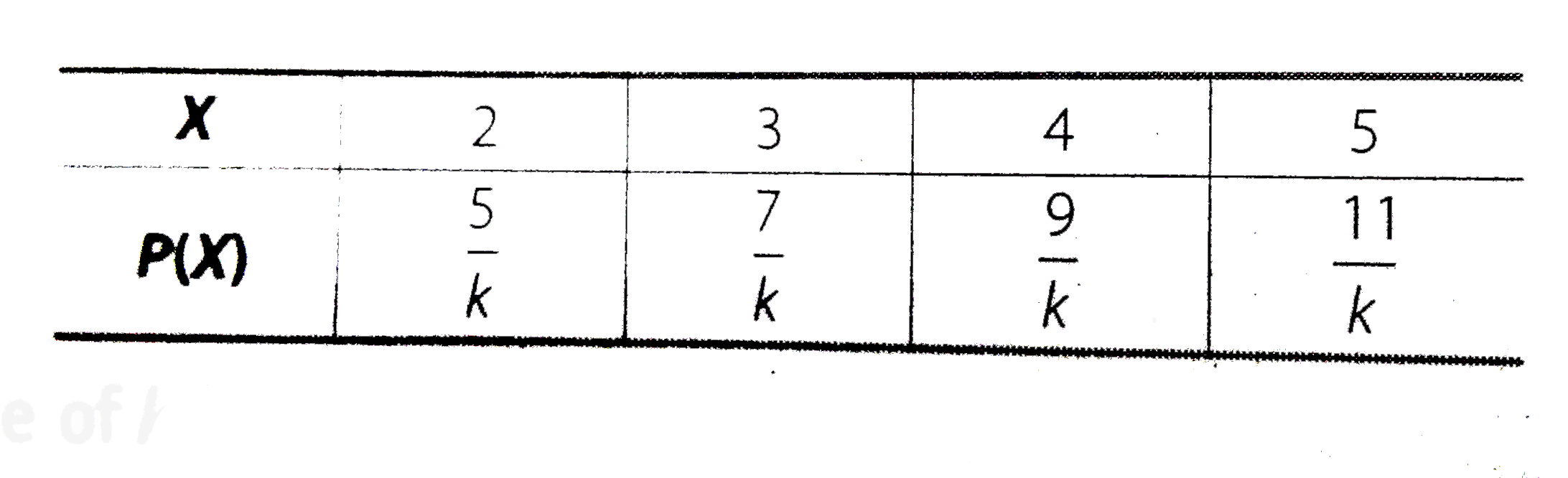
The value of k isA8B16C32D48The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2
If the probability distribution of a random variable X is as given below
Then, mean and variance are

View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is a. 8 b. 16 c. 32 d. 48
View SolutionThe probability distribution of a discrete random variable x is given as under
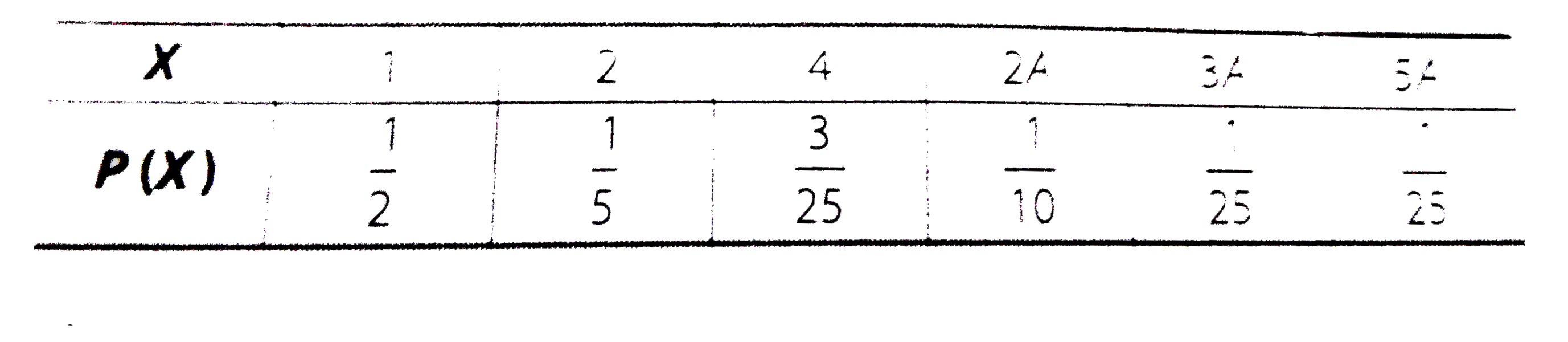
Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.
View SolutionThe probability distribution of a random variable x is given below: What is the standard deviation of x?
View SolutionThe probability distribution of discrete random variable X is given below
x2345P(x)5K7k9k11k
find the value of K.
View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)
View Solution