Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
The correct Answer is:x2+y2=4r2
Let the point of intersection of tangents at A and be P≡(x,y) .
Since AB=AO=BO=r, we get
∠AOB=60∘
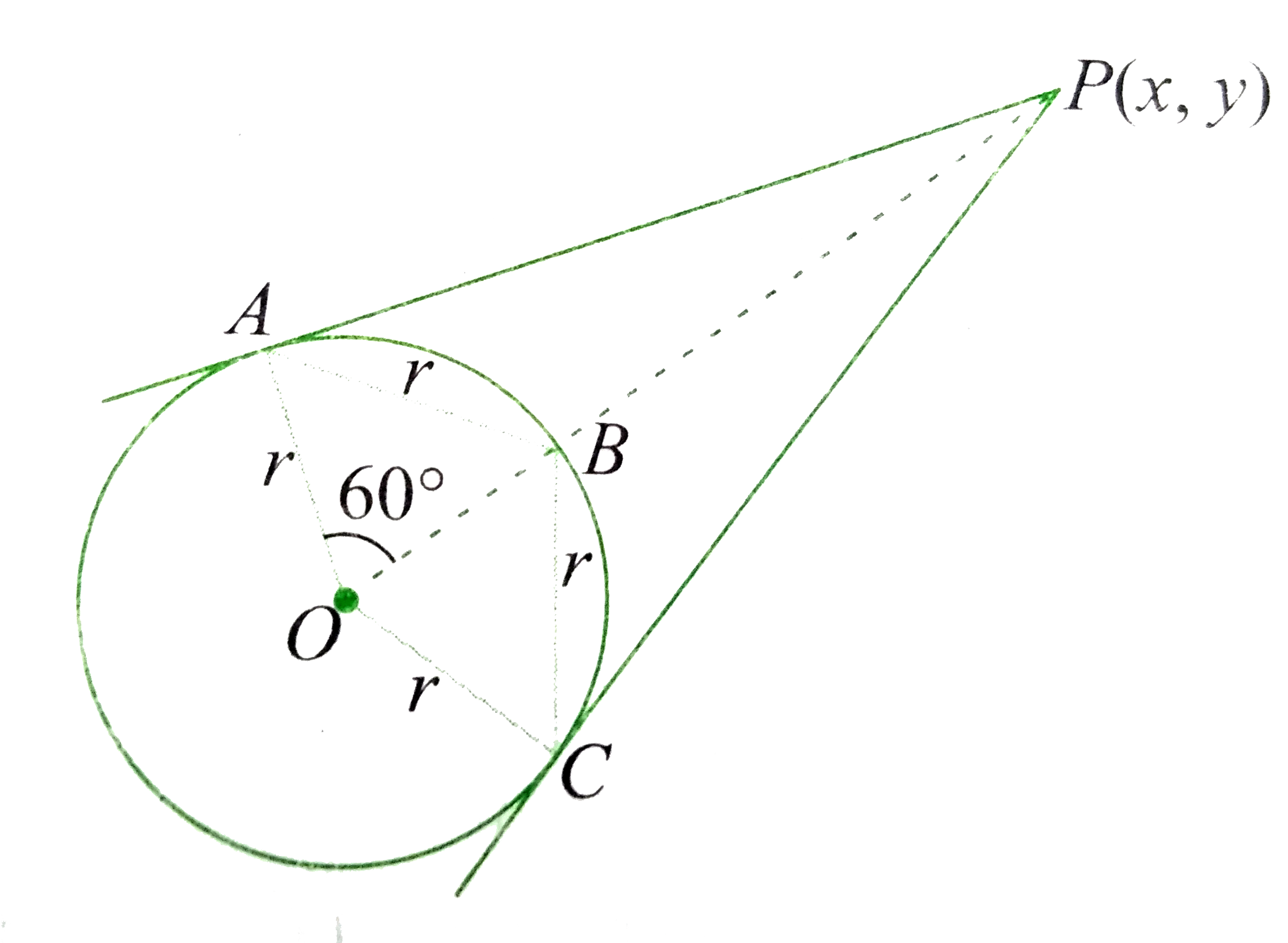
or PArtan60∘=√3
or √x2+y2−r2=√3r
Therefore, x2+y2=4r2 is the locus of the point P.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.4
14 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.5
12 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.2
5 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a ,then locus of point of intersection of tangents at A and C is a circle of radius λa, where λ is
View Solution
Knowledge Check
A chord AB of circle x2+y2=a2 touches the circle x2+y2−2ax=0.Locus of the point of intersection of tangens at A and B is :
Ax2+y2=(x−a)2Bx2+y2=(y−a)2Cx2=a(a−2y)Dy2=a(a−2x)Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C isAx2+y2=a2Bx2+y2=2a2Cx2+y2=4a2Dx2+y2=8a2A chord AB of circle x2+y2=a2 touches the circle x2+y2−2ax=0.Locus of the point of intersection of tangens at A and B is :
Ax2+y2=(x−a)2Bx2+b2=(y−a)2Cx2=a(a−2y)Dy2=a(a−2x)
From an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at AandB . The locus of the point of intersection of tangents at AandB to the circle x2+y2=9 is x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of these
View SolutionA variable chord of the parabola y2=8x touches the parabola y2=2x. The the locus of the point of intersection of the tangent at the end of the chord is a parabola. Find its latus rectum.
View SolutionIf there are two points AandB on rectangular hyperbola xy=c2 such that abscissa of A= ordinate of B, then locusof point of intersection of tangents at AandB is (a) y2−x2=2c2 (b) y2−x2=c22 (c) y=x (d) non of these
View Solutionif a variable tangent of the circle x2+y2=1 intersects the ellipse x2+2y2=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is
View SolutionA variable chord PQ of the parabola y=4x2 subtends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is
View Solution
