limn→01n⎛⎜⎝c∫yesin2tdt−x∫x+ysin2tdt⎞⎟⎠ is equal to (c being constant) :
A
esin2y
B
sin2yesin2y
C
0
D
None of these.
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- UNIT TEST PAPER NO. 2 (GEOMETRIES)BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST PAPER NO. 2 (GEOMETRIES)EXERCISE - Select the correct answer
25 Videos
- UNIT TEST PAPER NO. 6 (THREE - DIMENSIONAL GEOMETRY, VECTORS & PROBABILITY)BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST PAPER NO. 6 (THREE - DIMENSIONAL GEOMETRY, VECTORS & PROBABILITY)EXERCISE - Select the correct answer
25 Videos
Similar Questions
Knowledge Check
limx→01x[∫0yesin2tdt−∫0x+yesin2tdt] is equal to:
Aesin2yBsin2yesin2yC0Dnone of theselimx→01x[∫ayesin2tdt−∫ax+yesin2tdt] is equal to
Aesin2yBsin2yesin2yC0DNone of theselimx→0∫x0ttan(5t)dtx3 is equal to :
A−43B−53C43D53
limx→0∫x0ttan(5t)dtx3 is equal to :
View SolutionThe value of .nC0n+.nC1n+1+.nC2n+2+...+.nCn2n
(a)1∫0xn−1(1+x)ndx (b)2∫1xn(x−1)n−1dx (c)2∫1(1+x)ndx
(d)1∫0(1−x)nxn−1dx
View SolutionLet LimT→∞1TT∫0(sinx+sinax)2dx=L then
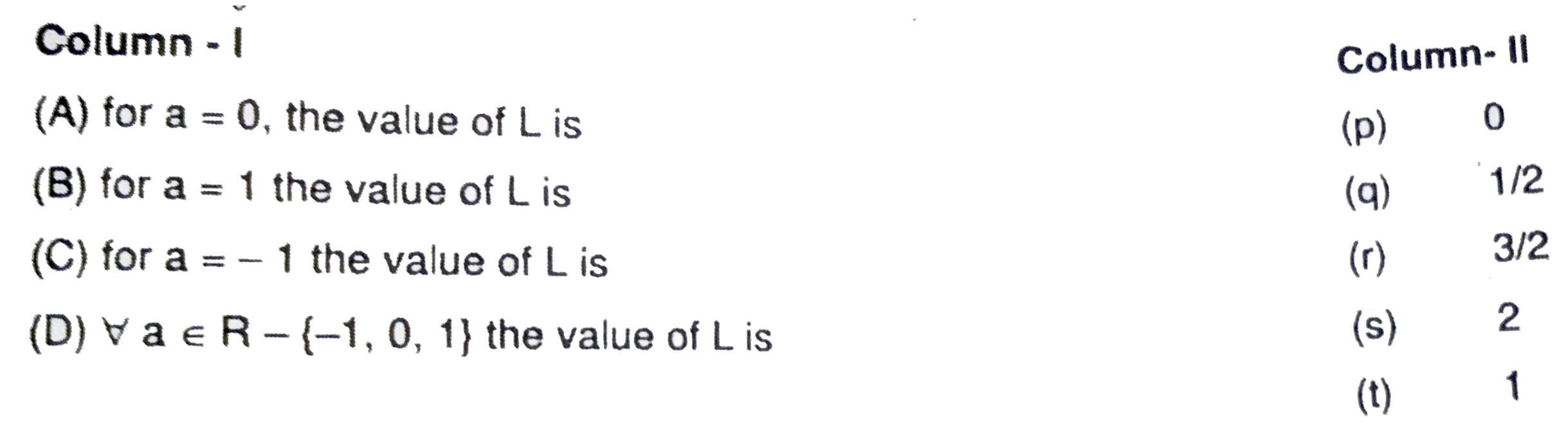
View SolutionThe value of
sin2x∫0sin−1√tdt+cos2x∫0cos−1√tdt, is
View SolutionFor x∈(0,5π2) define
f(x) = x∫0√tsintdt
Then has :
View Solution
