Use Euclid's division algorithm to find the HCF of (i) 135 and 225 (ii) 196 and 38220 (iii) 867 and 255
Video Solution
Text Solution
(i) Here , 225>135
divide 225 by 135 to get 1 as quotient and 90 as remainder .
∴ 225=135×1+90
Now the remainder is 90 which is not equal to zero
Again , divide 135 by 90 to get 1 as quotient and 45 as remainder
∴ 135=90×1+45
Again divide by 90 by 45 to get 2 as quotient and zero as remainder
∴ 90=45×2+0
Alternative method : It can also be shown in the following way
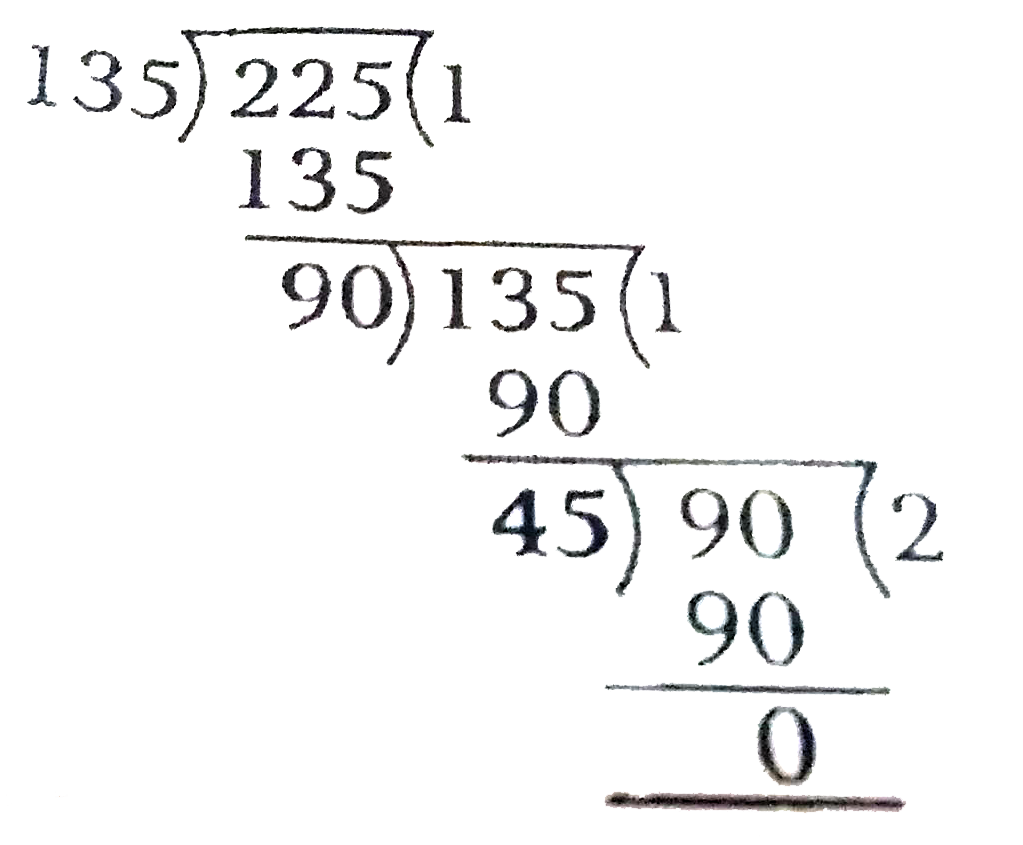
∴ 225=135×1+90
135=90×1+45
90=45×2+0
Since , remainder = 0 ⇒ recent divisor in the H.C.F.
∴ H.C.F. (225, 135) = 45
(ii) Here , 38220>196

∴ 38220=196×195+0
∵ the remainder is zero ⇒ recent divisor is the H.C.F.
∴ H.C.F. (38220 , 196) = 196
(iii) Here , 867>255
∴
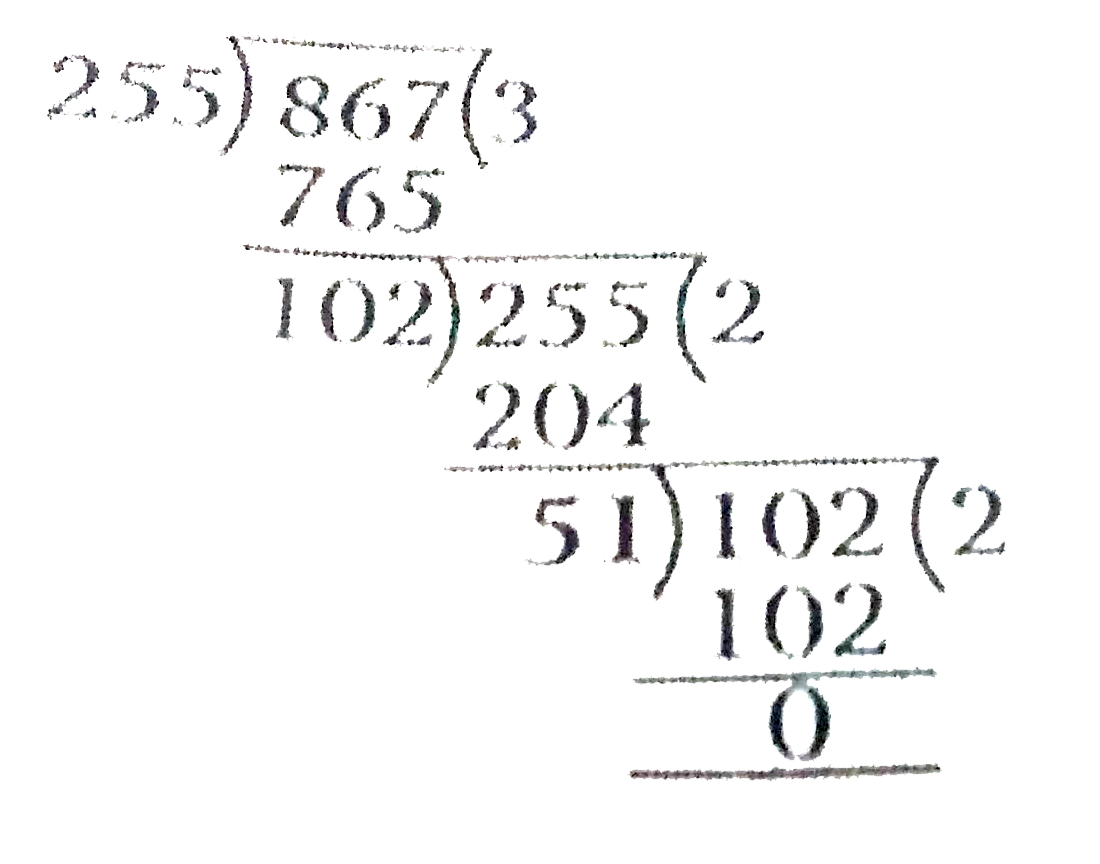
∴ 867=255×3+102
255=102×2+51
102=51×2+0
Since remainder =0⇒ recent divisor is the H.C.F.
∴ H.C.F. (867,255)=51
|
Topper's Solved these Questions
- REAL NUMBERSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - REAL NUMBERSEXERCISE - Solved Example
15 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - REAL NUMBERSEXERCISE - Problems From NCERT/ Exemplar
11 Videos
- QUADRATIC EQUATIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRATIC EQUATIONSEXERCISE - Revision Exercise Long Answer Questions
6 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
Find the H.C.F. of " 12, 18, 46
A2B4C6DNone of these
Use Euclid division algorithm to find the HCF of 441, 567 and 693.
View SolutionUse Euclid division algorithm to find the HCF of 441, 567 and 693.
View SolutionEuclid algorithm to find the H.C.F of 408 and 1032.
View SolutionUse Euclid's division algorithm , to find the H.C.F. of the following : (i) 70 and 40 (ii) 18 and 45
View SolutionUse Euclid's algorithm to find the H.C.F. of 4052 and 12576.
View SolutionUse Euclid's algorithm to find the H.C.F. of 4052 and 12576.
View SolutionUsing Euclid’s algorithm find the H.C.F. of 513 and 783
View Solution
