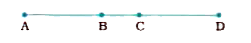Use the information marked to prove :
(i) ΔEAC≅ΔDBC (ii) EC=DC
Also state the Euclid's axiom used in proving the congruency of two triangles.
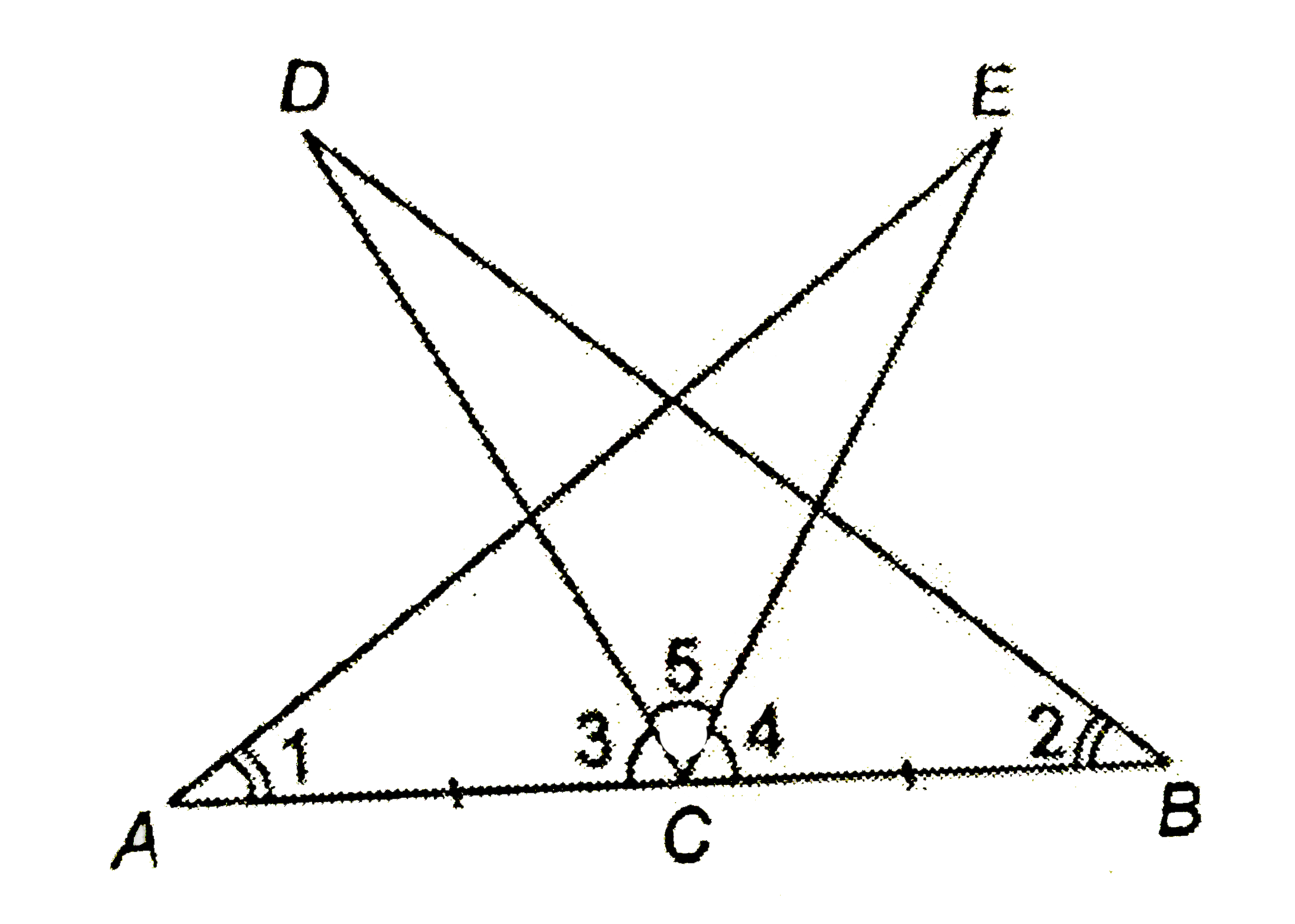
(i) We have ∠3=∠4 (given)
⇒∠3+∠5=∠4+∠5
(adding same angle on both sides)
This is the second axiom of Euclid : If equals are added to equals, the wholes are equal.
⇒∠ACE=∠BCD
Now, in ΔEAC and ΔDBC,
∴⎧⎪⎨⎪⎩∠ACE=∠BCD(just proved)AC=BC(given)∠EAC=∠CBD(given)
∴ΔEAC≅ΔDBC (ASA) Hence Proved.
(ii) Therefore, EC=DC (by c.p.c.t) Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Knowledge Check
ABCD is an isosceles trapezium . ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. AE and BF are the perpendicular drawn to CD. The congruence property used to prove the congurence of triangles AED and BFC is ______
ARHSBSASCSSSDASAABCD is an isosceles trapezium . ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. AE and BF are the perpendicular drawn to CD. The congruence property used to prove the congurence of triangles AED and BFC is ______
ARHSBSASCSSSDASAIn ΔPQRandΔABC, ∠Q=∠B=90∘,PQ=AB,andQR=BC. Which of the following property can be used to prove the congruence of ΔPQR and ΔABC ?
ASSSBRHSCASADSAS
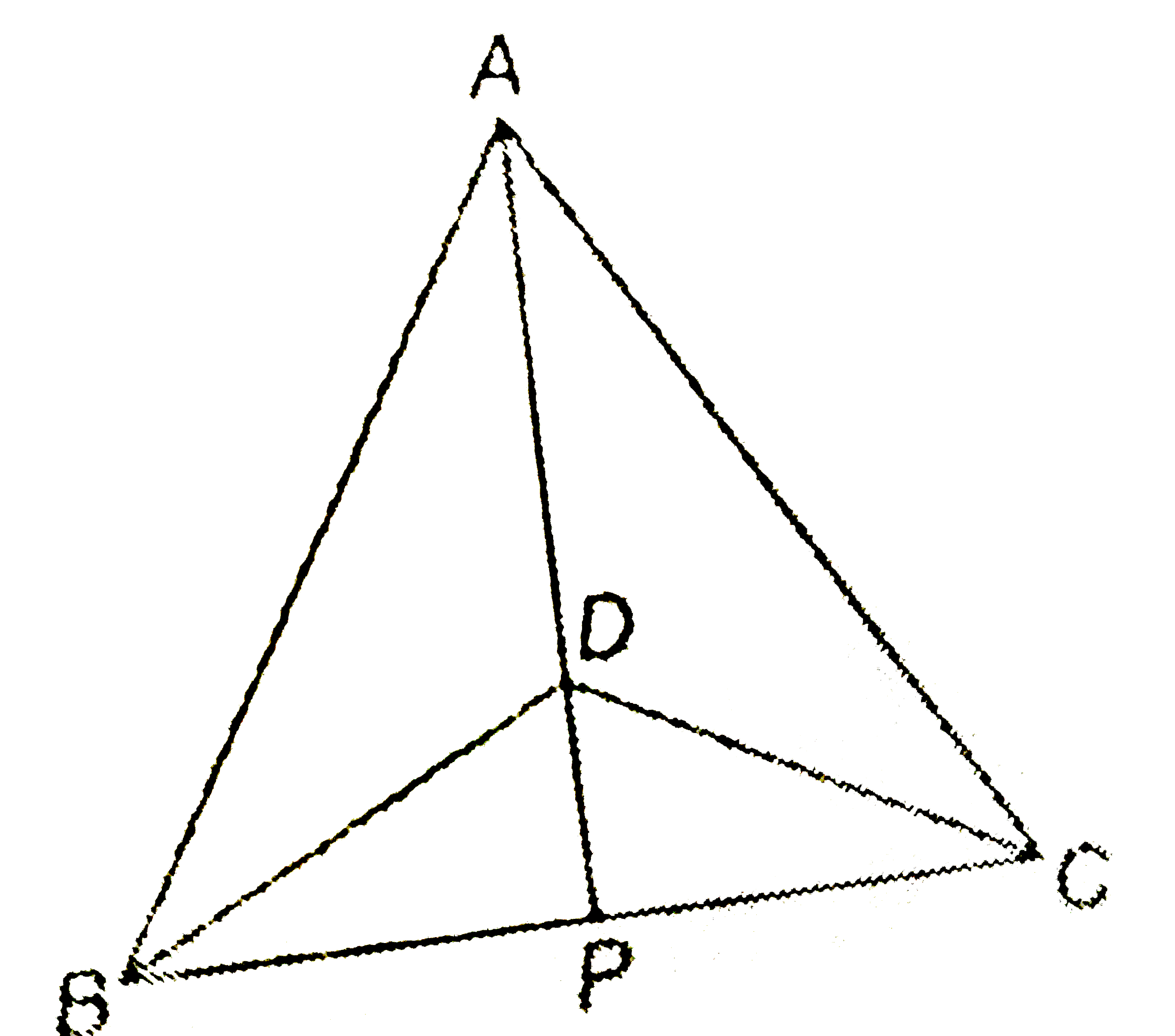
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
View Solutioni) Area of the rectangle = (length × breadth)
ii) Perimeter of the rectangle = 2 (length + width)
Use the above information to solve the following
The area of a rectangle is 24 cm2. The width is two less than the length. Find the length and width of rectangle.
View SolutionAttempt to prove Euclid 's fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
View SolutionLine-segments AB and CD bisect each other at O. AC and BD are joined forming triangles AOC and BOD. State the three equality relations between the parts of the two triangles that are given or otherwise known. Are the two triangles congruent? State in symbolic form, which congruence condition do you use?
View SolutionIn the given figure C is the midpoint of AB,D is the midpoint of XY and AC=XD Using an Euclid 's axiom prove that AB =XY
View Solution