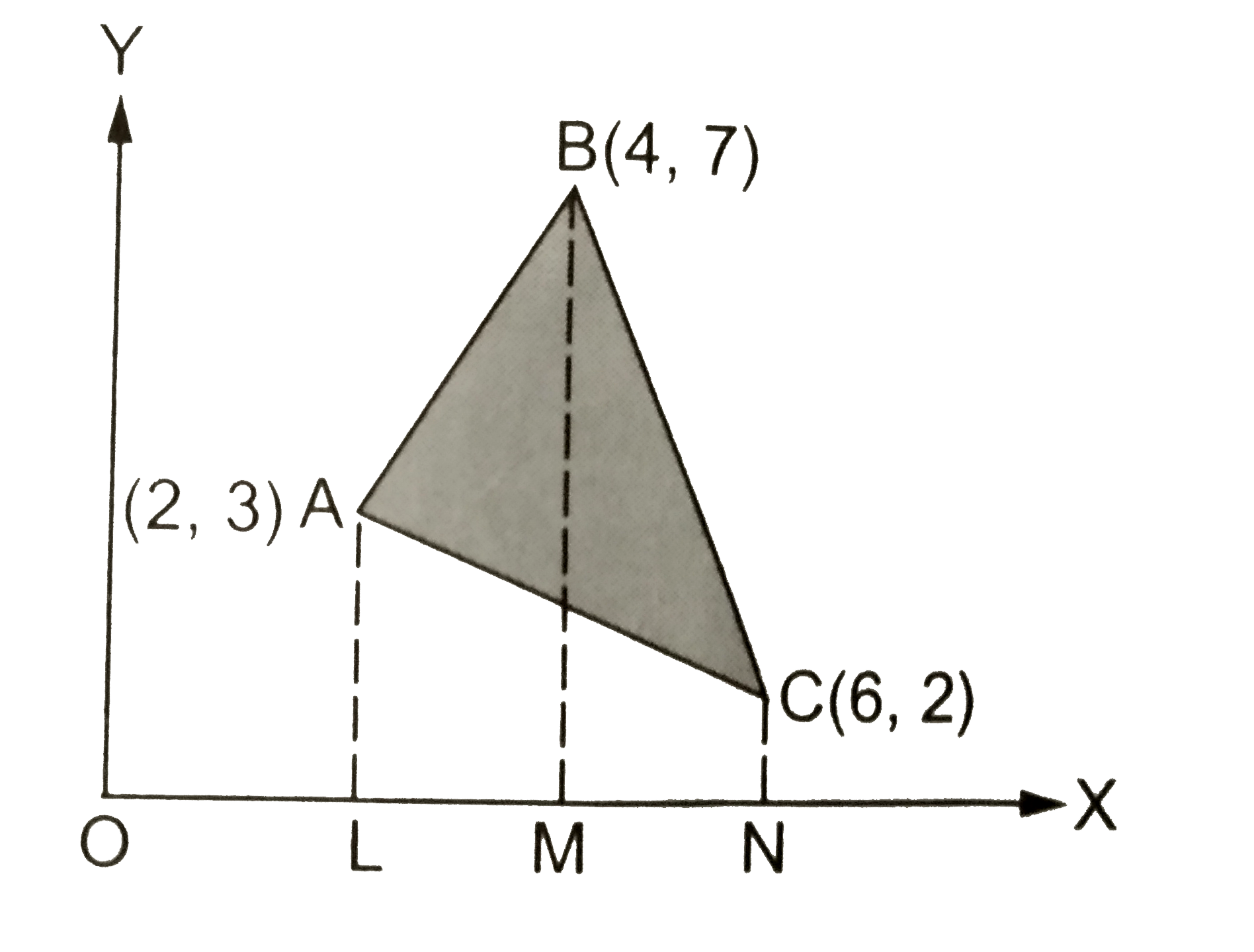
Using integration, find the area of $Δ A B C$ , whose vertices are $A (2, 3), B (4, 7)$ and $(6, 2)$ .

Video Solution

Text Solution

Verified by Experts

The equation of AB is
$\frac{y - 3}{x - 2} = \frac{7 - 3}{4 - 2} \Rightarrow y = 2 x - 1$
The equation of BC is $\frac{y - 7}{x - 2} = \frac{2 - 3}{6 - 2} \Rightarrow y = \frac{- 1}{4} x + \frac{7}{2}$
Draw $A L ⊥ O x, B M ⊥ O X and C N ⊥ O X$
Area of $Δ$ ABC=(area ALMBA+ are BMNCB)-(area ALNCA)
$= 4 \int 2 y A B d x + 6 \int 4 y a B C d x - 6 \int 2 y A C d x$
$= 4 \int 2 (2 x - 1) d x + 6 \int 4 (- \frac{5}{2} x + 17) d x - 6 - \frac{1}{4} x + \frac{7}{2} 2 d x$
$= {[x^{2} x]}_{2}^{2} + {[- \frac{5}{4} x^{2} + 17 x]}_{4}^{2} - {[- \frac{1}{8} x^{2} + \frac{7}{2} x]}_{2}^{2}$
$= [(12 - 2) + (57 - 48) - (\frac{33}{2} - \frac{13}{2})]$ sq units
= 9 sq units
Hence the required area is 9 sq units .

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of $Δ A B C$ whose vertices are A (2,5), B (4,7) and C(6,2) is
A7 sq. units
B14 sq. units
C21 sq. units
D28 sq. units
Find the area of the triangle, whose vertices are (2,1), (4,5) and (6,3).
A $3$
B $6$
C $9$
D $12$

RS AGGARWAL-AREA OF BOUNDED REGIONS -Exercise 17

Home
Ask Doubt
Profile