Using integration, find the area of the region bounded by the lines, 4x−y+5=0;x+y−5=0 and x−4y+5=0
Video Solution
Text Solution
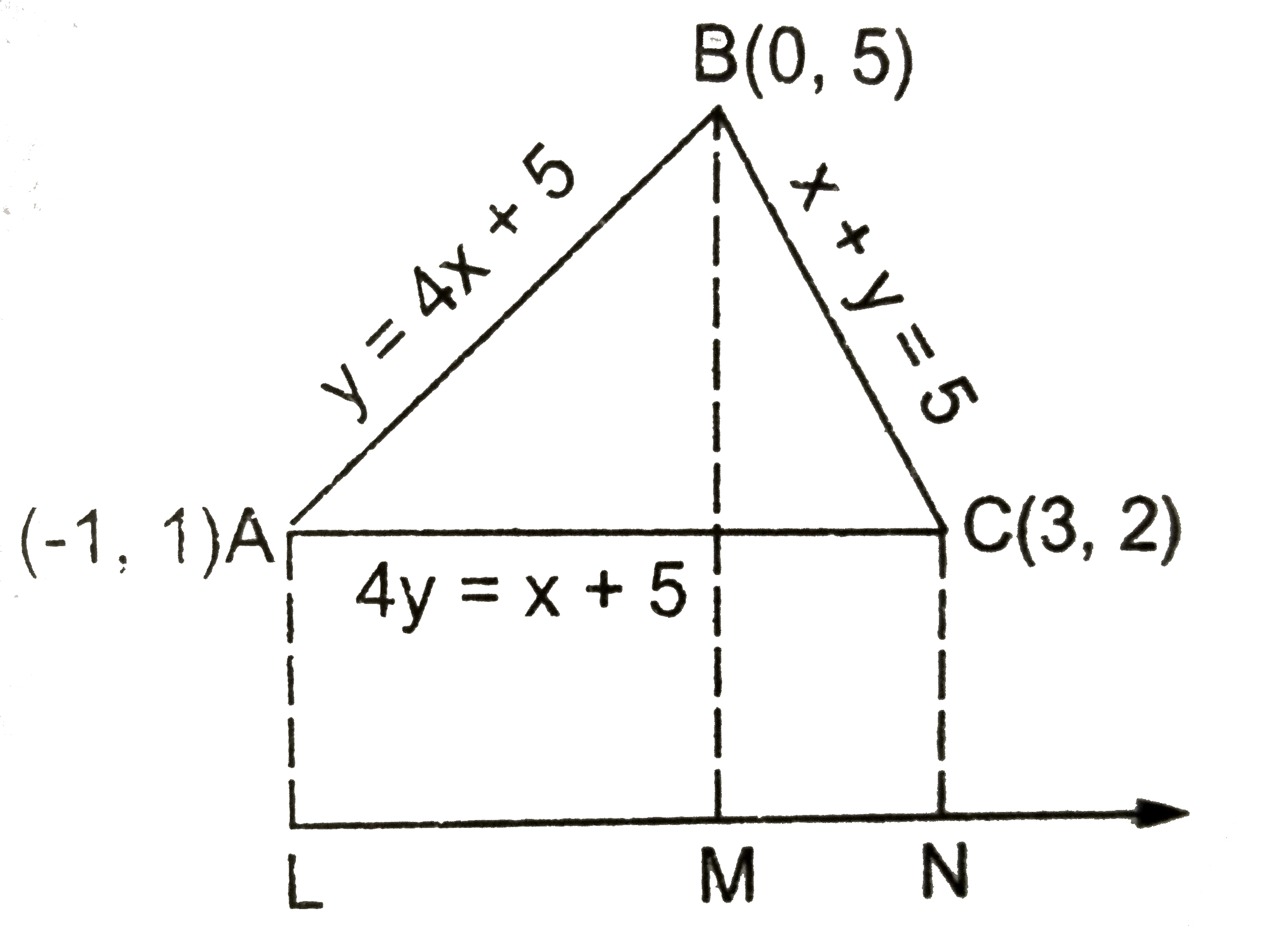
Solving the given equations in pairs , we get the points (A-1,1),B (0,5) and C (3,2)
Draw AL,BM and CN perpendiculars on the x-axis
Required area
=0∫−1y AB dx+3∫0y BC dx−14.3∫−1 y CA dx
=0∫−1(4x+5)dx+3∫0(−x+5)dx−14.3∫−1(x+5)dx
|
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
Using the method of integration, find the area of the region bounded by the lines 5x−2y−10=0,x+y−9=0and2x−5y=0
A10 sq. unitsB10.5 sq. unitsC11 sq. unitsDNone of theseWhat is the area of the region bounded by the lines y=x,y=0 and x=4 ?
A4 square unitsB8 square unitsC12 square unitsD16 square unitsWhat is the area of the region bounded by the lines y=x.y=0 and x=4?
A4 sq. unitsB8 sq. unitsC12 sq. unitsD16 sq. units
Find by integration, the area of the triangle bounded by the lines 4y-5x=0 and x=4.
View SolutionUsing the method of integration, find the area of the region bounded by the lines 3x − 2y+1=0, 2x+3y − 21=0 and x − 5y+9=0.
View SolutionUsing the method of integration, find the area of the region bounded by the lines : 2x+y=4 3x − 2y=6 x − 3y+5=0
View SolutionUsing integration, find the area of the region bounded by the line xy+2=0 , the curve x=√y and y−aξs.
View SolutionUsing integration, find the area of the region bounded by the curve y2=9x and lines x=1 and x=4.
View Solution
