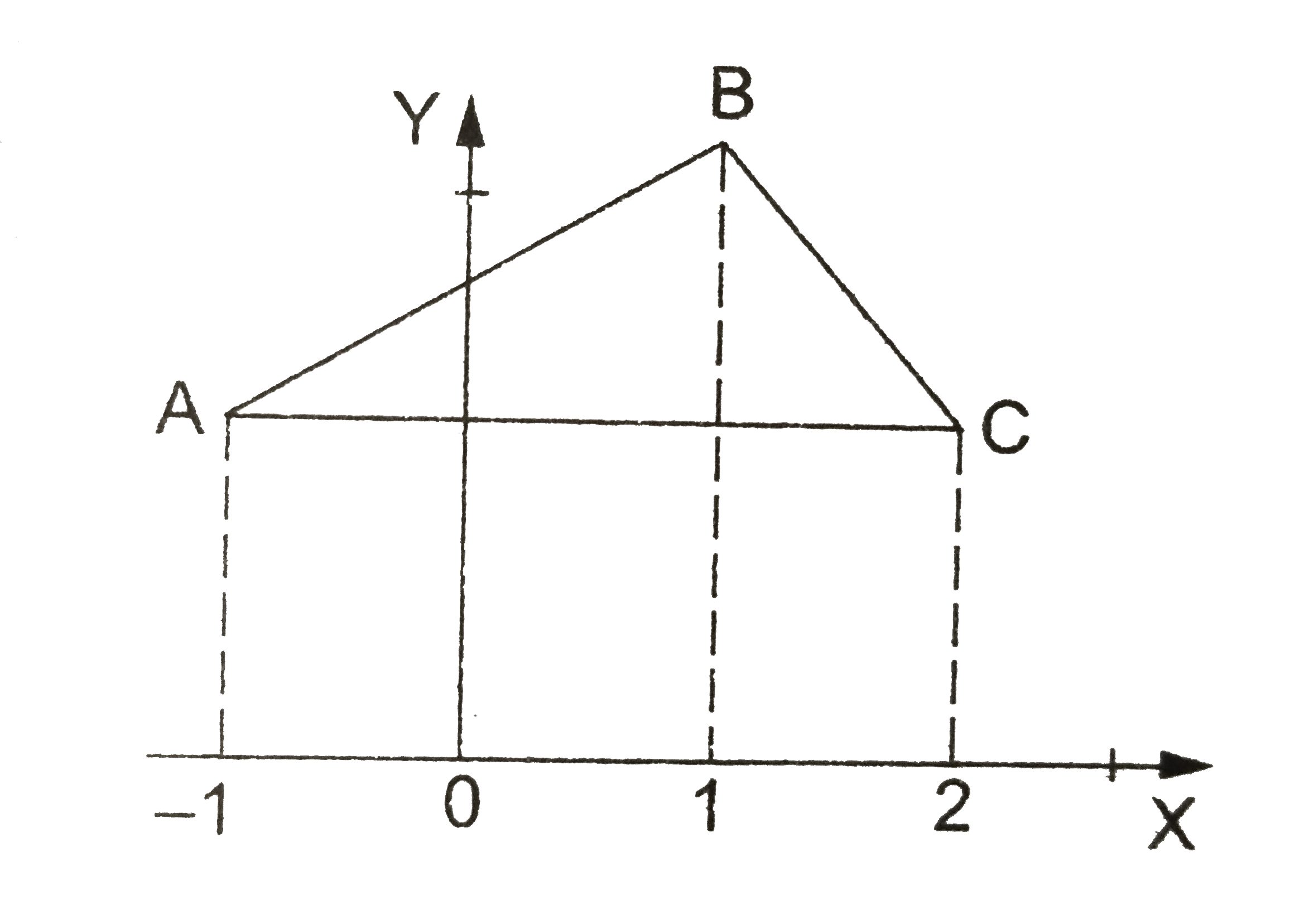
Using integration, find the area of the region bounded by the triangle whose vertices are (−1,2),(1,5)and(3,4).
Equations of AB,BC and AC are
y=12(3x+7),y=12(11−x)
and y=12(3x+7),y=12(11−x)
and y=12(x+5) respectively
∴Δ=121∫−1(3x+7)dx+123∫1(11−x)dx−123∫1(x+5)dx
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Using integration find the area of region bounded by the triangle whose vertices are (1,0),(1,3)and(3,2).
View SolutionUsing integration find the area of region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1).
View SolutionUsing integration, find the area of region bounded by the triangle whose vertices are (–2,1),(0,4)and(2,3).
View SolutionUsing integration find the area of the region bounded by y2=4ax and x=4a
View SolutionUsing intergration find the area of the area of the triangle whose vertieces are A(1,3), B(2,5)and C( 3,4)
View SolutionUsing integration, find the area of the triangle ABC whose vertices are A(−1,1),B(0,5) and C(3,2).
View SolutionUsing integration, find the area of the triangle whose vertices are (−1,0)(1,3) and (3, 2).
View SolutionUsing integration, find the area of the region bounded by the parabola y2=16x and the line x=4
View SolutionFind the area of the triangle whose vertices are A(1, 2, 3), B(2, –1, 1)and C(1, 2, –4).
View SolutionFind the area of the triangle whose vertices are (-3, 1), (2,4) and (5, 1).
View Solution
