Using integration find the area of the triangular region whose sides have equations y=2x+1, y=3x+1 and x=4
Video Solution
Text Solution
y= 2x +1 is the line passing through A(−12,0) and B (0,1)
y=3x + 1 is the passing through C(−13,0) and B (0,1)
x= 4 is the parallel to y-axis and passing through D(4,0)
Required area= (area ODFB))-(area ODEB)
=4∫0(3x+1)dx−4∫0(2x+1)dx
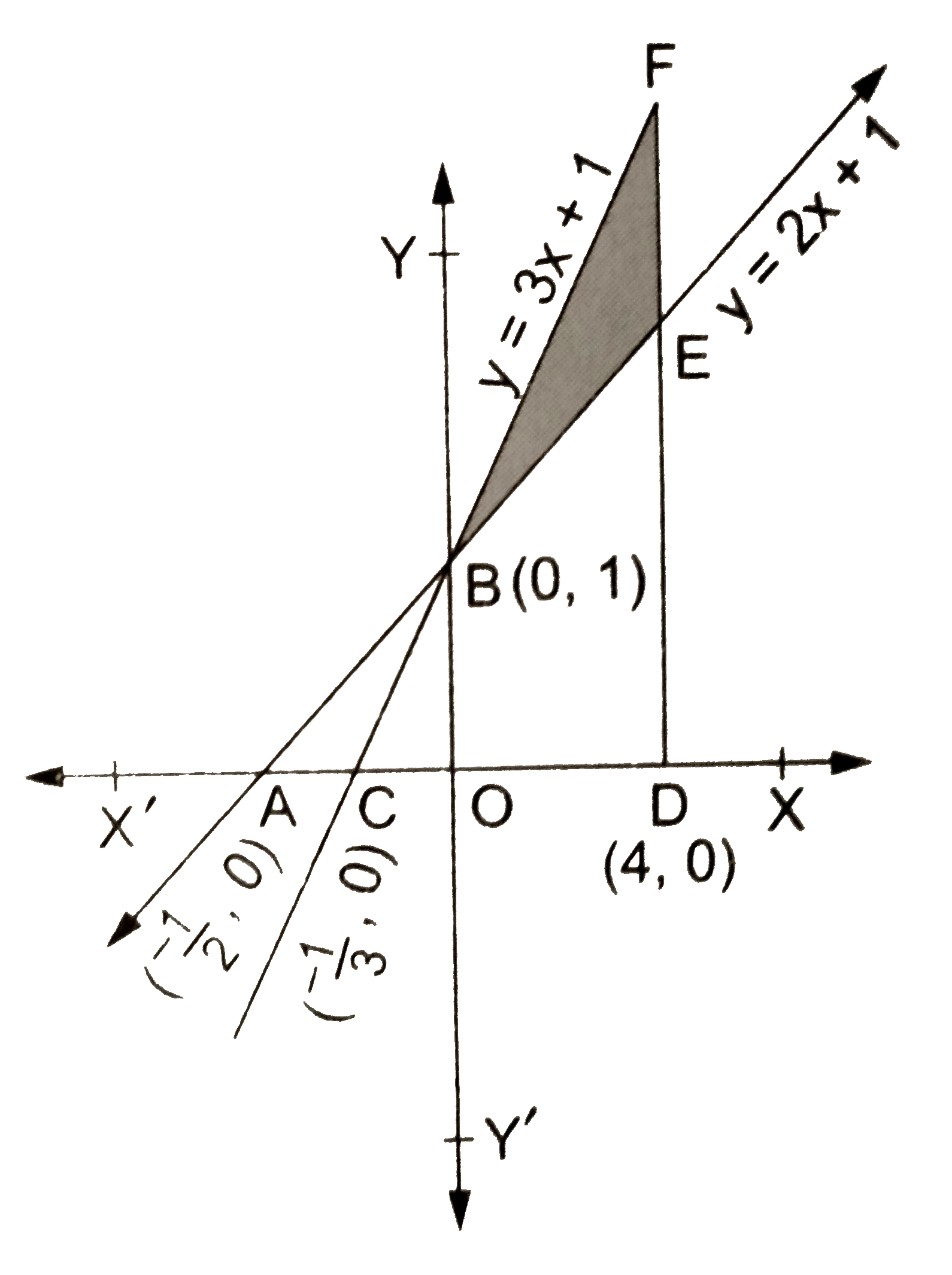
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions89videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 3018videos
BAYES'S THEOREM AND ITS APPLICATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the orthocentre of the triangle whose sides have the equations y = 15, 3x = 4y, and 5x + 12y = 0.
A(0, 0)B(0, -33)C(- 33, 33)D(- 33, 0) - Question 2 - Select One
Find the area of the triangle formed by the straight lines whose equations are 2y+x−5=0,y+2x−7=0, and x−y+1=0.
A310B10C6D25 - Question 3 - Select One
Find the area of the triangle formed by the straight lines whose equations are 2y+x−5=0,y+2x−7=0, and x−y+1=0.
Aa. 32Bb. 10Cc. 6Dd. 25
Using integration find the area of the region bounded by y2=4ax and x=4a
View SolutionFind the area of the triangle, the equations of whose sides are y=x, y=2x and y-3x=4.
View SolutionFind the vertices and the area of the triangle whose sides are x=y,y=2xandy=3x+4.
View SolutionUsing integration, find the area of the region: {(x,y):9x2+y2≤36 and 3x+y≥6}
View SolutionUsing intergration, find the area of the region bounded by the lines y=|x+1|,x=−3,x=1 and X-axis.
View Solution

