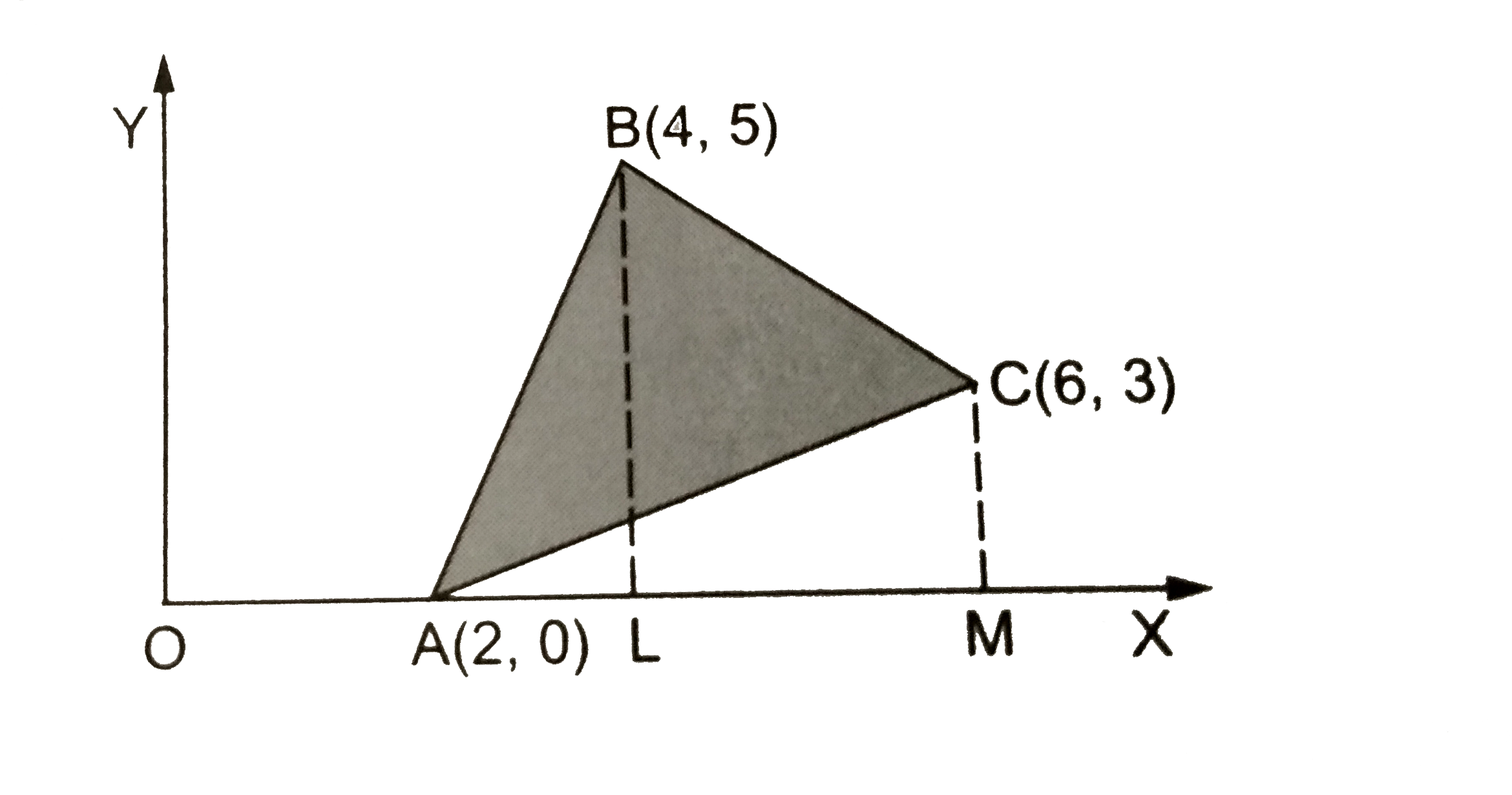
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
The equation of side AB is
y−0x−2=5−04−2⇒y−52(x−2)
The equation of side BC is
y−5x−4=3−56−4⇒y=−x+9
The equation of side AC is
y−0x−2=3−06−2⇒y=34(x−2)
Draw perpendiculars BL and CM on the x-axies
∴ area of ΔABC
=ar(ΔALB)+ar(trap.BLMC)−ar(ΔAMC)
=2∫4yABdx+6∫4(9−x)dx−346∫2yBCdx−6∫2yACdx
=524∫2(x−2)dx+6∫4(9−x)dx−346∫2(x−2)dx
=52[x22−2x)]42+[9x−x22]64−34[x22−2x]62
=52[0−(−2)]+(36−28)−34[6−(2−)]
= (5+8−6) sq units = 7 sq units
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
The area of ΔABC whose vertices are A (2,5), B (4,7) and C(6,2) is
A7 sq. unitsB14 sq. unitsC21 sq. unitsD28 sq. units
Using integration, find the area of the triangle PQR, coordinates of whose vertices are P(2, 0), Q(4, 5) and R(6, 3).
View SolutionUsing the method of integration, find the area of the triangular region whose vertices are (2,−2),(4,3)and(1,2).
View SolutionUsing integration, find the area of the triangle ABC whose vertices are A(−1,1),B(0,5) and C(3,2).
View SolutionUsing intergration find the area of the area of the triangle whose vertieces are A(1,3), B(2,5)and C( 3,4)
View SolutionUsing integration find the area of region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1).
View SolutionFind the area of the quadrilateral whose vertices are A (0, 0), B (6, 0), C (4, 3) and D (0, 3).
View SolutionUsing integration find the area of region bounded by the triangle whose vertices are (1,0),(1,3)and(3,2).
View Solution
