Volume and surface area of cylinder
Volume and Surface Area of Cylinder
The area occupied by a three-dimensional space in a cylinder is the surface area of a cylinder. The cylinder will have circular bases that are parallel to each other. The cylinder can be observed as a set of circular disks that which are stacked on one by another, making it look like a hollow object called as a cylinder. Being a three-dimensional shape and object, the cylinder has the surface area and a volume.
The cylinder has two types of surfaces. Among these surfaces, one is a curved surface, and the other is the surface that will include the area of two circular bases as well. Hence, if one needs to find out the total surface area of the cylinder, he or she should calculate it by calculating the sum of the both the curved surface area and the area of circular bases. Not only the total surface area of the cylinder is calculated like that, but even the volume of the cylinder is also calculated in a similar manner by adding together the circular and lateral surfaces.
Total Surface area of cylinder formula
The total region that is being covered by the cylinder in the three dimensional space is called the Total surface area of the cylinder. Basically, this area of this portion can be calculated by adding together the area of the two circular bases and the curved surface area of the cylinder. The total region covered by the cylinder in the particular three dimensional spaces in called as the area of the cylinder and the total surface area of the cylinder. The total area of the Volume and surface area of cylinder and total surface area of the cylinder is that which is equal to the sum of area of two circular bases and the curved surface area.
Total Surface Area of Cylinder = Curved Surface Area + Area of Circular bases
TSA = 2πr (h + r)
There is another name of the curved surface. This curved surface is also known as the lateral surface. There will be a curved surface in the midst of the two circular bases, and if it is opened there will come a rectangular shape. Using these shapes one can easily notice an independent surface area and which is called as a rectangular shape.
Area of a Cylinder Formula
The classification of the surface area of the cylinder can be easily made into two types, which is typically made into two types
- Curved Surface Area
- Total Surface Area
Curved Surface Area
The area of the curved surface area for any given cylinder with a radius of r and height represented by ‘h’ is also known as the lateral surface area and that is shown as LSA. The curved surface area of cylinder is also called as the lateral surface area and that is referred to as the LSA. The formula of the curved surface area of that cylinder is given by the radius “r “ and that the height is shown as h.
CSA or LSA = 2π r h Sq. units
Total Surface Area of Cylinder
The sum of areas of all the faces of the cylinder is called as the total surface area of the cylinder and is equal to the adding up together of the sum of curved surface area and circular bases of the cylinder. For the total surface area of the cylinder, the radius is represented by ‘r’ and the height is denoted by ‘h’. The height which is denoted by h will always be greater and be equal to the curved area and the circular areas of the cylinder.
Total Surface Area of Cylinder = Curved Surface Area of cylinder + Area of Circular bases of cylinder
TSA = 2πr (h + r) square units
Where, π (Pi) = 3.142
Related Videos:
- Volume and Total surface area of cuboid
- Volume and surface area of cube
- Volume and surface area of cone
- Volume and surface areas of sphere
- Volume and surface area of pyramid
Understanding Surface Area of Cylinder
First let us assume that the paint needs to be applied to a particular shaped object that which is the shape of a cylinder container that is in the shape of a cylinder. The painting need to be applied to all the faces of the container, beforehand we need to find out the quantity of paint that is required to paint the total area of the cylindrical container. This means we need to paint the total area of all the walls and faces of the container need to be painted with red or green colours.
Let us assume that the base radius of the cylinder base is represented by r and the height of the cylinder is represented by h units. This means that the radius of the cylinder is represented by r and the height of the volume of cylinder formula is represented by h units. The curved surface of the cylinder will be having when opened the container will be having a diameter of 2r, in which the radius is represented by r and the height is represented by h units. The formula for the diameter of the cylinder is d=2r in which radius is represented by r, and the height is represented by h.
For the figure given below, when the curved surface of cylinder is opened, the cylinder will open into the form a rectangle shape. The area of the rectangle will have a height and circumference dimensions of the cylinder and the formation is a bit peculiar.
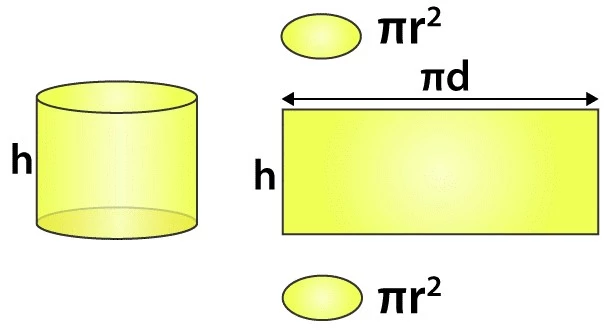
The formula for the total surface area of a given cylinder with radius ‘r’ and height ‘h’, is
TSA = 2πr (h + r)
Important Chapters:

Similar Questions
If the volume and curved surfaces area of a cylinder are 616 m3 and 352 m2 respectively, what is the total surface area of the cylinder (in m2) (a) 429 (b) 419 (c) 435 (d) 421 (e) 417
View SolutionThe volume and the curved surface area of a cylinder are 1650cm3and660cm2 respectively. Find the radius and height of the cylinder.
View Solution
Knowledge Check
- Question 1 - Select One
A teacher has to teach the subject volume and surface area of a cylinder and a cone.
The skill based objective of teaching will beAthe pupil will be able to distinguish between features of a cylinder and a coneBthe pupil will be able to draw the figure of a cylinder and a coneCthe pupil will be able to recall the formulae for calculating volume and surface area of cylinder and coneDthe pupil will be able to find the height of a cone when a given cylinder is melted into cone - Question 2 - Select One
If the volume and curved surface area of a cylinder are 269.5cm3 and 154cm2 respectively , what is the height of the cylinder ?
A6B3.5C7Dcan't be determined - Question 3 - Select One
If the volume and curved surface area of a cylinder are 269.5cm3 and 154cm2 respectively , what is the height of the cylinder ?
A6B3.5C7Dcan't be determined
If curved surface area of cylinder is equal to its volume. What is the radius of cylinder?
View SolutionFind the volume, curved surface area and the total surface area of a cylinder with diameter of base 7 cm and height 40 cm.
View SolutionFind the volume, curved surface area and the total surface area of a cylinder with diameter of base 14 cm and height 80 cm.
View SolutionThe ratio of curved surface area of a right circular cylinder to the total area of its two bases is 2:1. If the total surface area of cylinder is 23100cm2, then what is the volume (in cm3) of cylinder?
View SolutionThe ratio of curved surface area of a right circular cylinder to the total area of its two bases is 2 : 1. If the total surface area of cylinder is 23100 cm2 , then what is the volume (in cm3 ) of cylinder?
View Solution
