We know that the sum of the interior angles of a triangle is1800 . Show that the sums of eth interior angles of polygons with 3,4,5,6, sides for an arithmetic progression. Find the sum of the interior angles of or a 21 sided polygon.
Video Solution
Text Solution
We know that sum of interior angles of a polygon of side n=(2n−4)×90∘=(n−2)×1802
Sum of interior angles a polygon with sides 3 is 180.
Sum of interior angles of polygon with side 4=(4−2)×180∘=3602
Similarly , sum of interior angles of polygon with side 5,6,7,. are 540∘,720∘,900∘.......
the series will be 180∘,360∘,540∘,720∘,900∘,......
Here a=180∘
andd=3602−180∘=180∘
since common difference is same between two consecutive terms of the series .
so ir from an AP .
we have to find the of interior angles of a 21 sides polygen .
it means , we have to find the 19 th term of the above series .
a19=a+(19−1)d
=180+18×180=3420
|
Topper's Solved these Questions
- SEQUENCE AND SERIESBOOK - NCERT EXEMPLARCHAPTER - SEQUENCE AND SERIESEXERCISE - long answer type questions
4 Videos
- SEQUENCE AND SERIESBOOK - NCERT EXEMPLARCHAPTER - SEQUENCE AND SERIESEXERCISE - Objective type Question
10 Videos
- RELATIONS AND FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False
5 Videos
- SETSBOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - TRUE AND FALSE
6 Videos
Similar Questions
Knowledge Check
The sum of the interior angle of a 10-sided polygon is _______
A1260∘B1440∘C1800∘D1620∘Find the sum of the interior angles of the polygon given below .
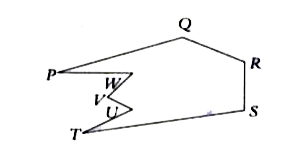 A1080∘B1440∘C1800∘D900∘
A1080∘B1440∘C1800∘D900∘The sum of the interior angle of a 10-sided polygon is _______
A1260∘B1440∘C1800∘D1620∘
Find the sum of the interior angles of the an 8-sided polygon.
View SolutionFind the sum of the interior angles of the an 8-sided polygon.
View SolutionFind the sum of the interior angles of a polygon of 8 sides.
View SolutionFind the sum of the interior angles of the polygon gives below.
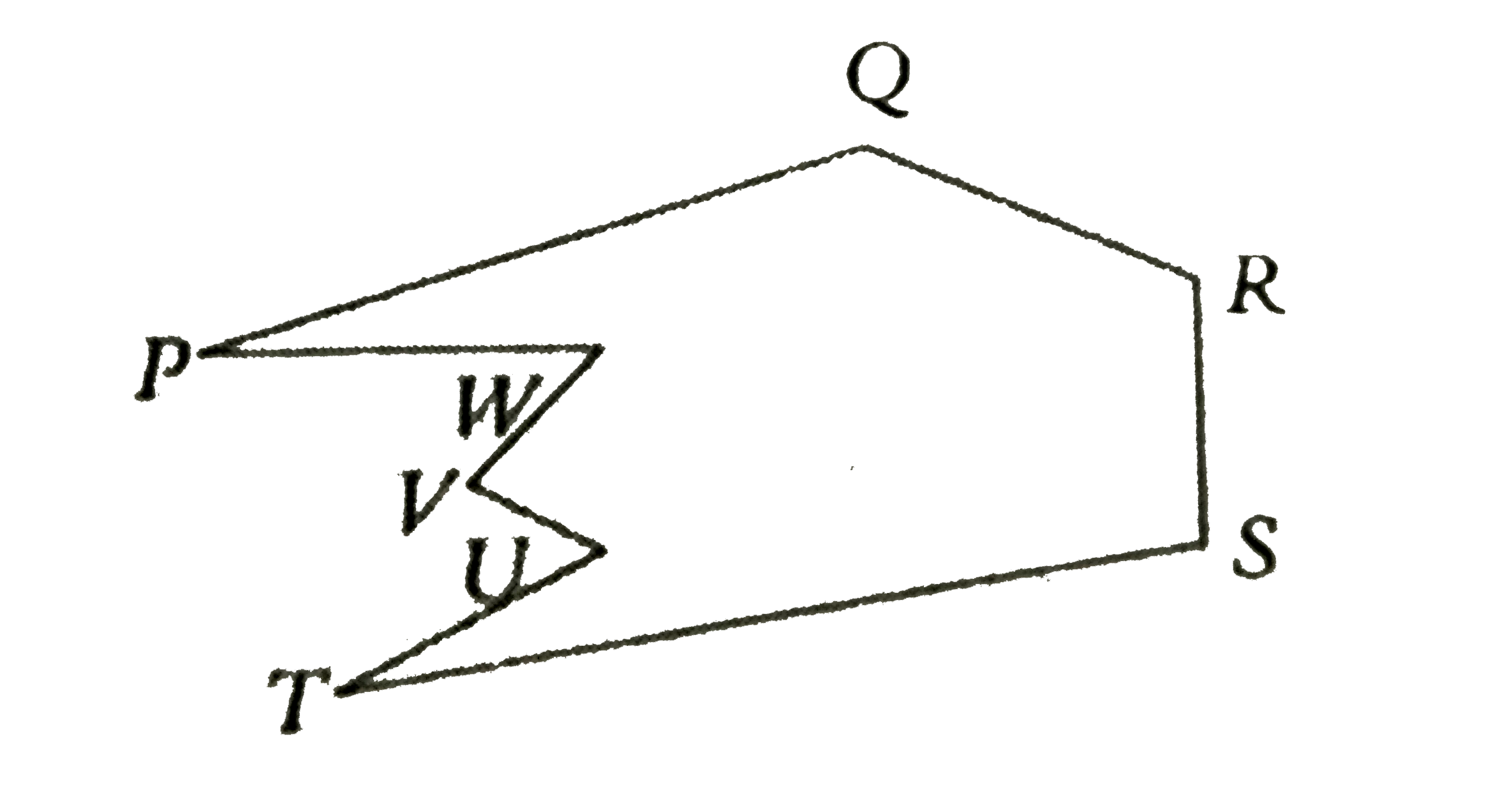
View SolutionProve that the sum of the interior angles of an octagon is twice the sum of interior angles of a pentagon
View Solution
