We know that the sum of the interior angles of a triangle is1800 . Show that the sums of eth interior angles of polygons with 3,4,5,6, sides for an arithmetic progression. Find the sum of the interior angles of or a 21 sided polygon.
Video Solution
Text Solution
The correct Answer is:3420∘
The sum of the interior angles of a triangle is 180∘ .A polygon of 4 sides can be divided into two triangles and therefore, the sum of its angles is 360∘ . A polygon of 5 sides can be divided into 3 tirangles and therefore, the sum of its angles (3×180∘)=540∘ and so on. Thus, a polygon of 21 sides is divided into (21-2) =19 triangles and therefore,the sum of its angles is (19×180∘)=3420∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 11B28videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 11C12videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Solved Examples16videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF CONIC SECTIONSEXERCISE - EXERCISE 255videos
APPLICATIONS OF CONIC SECTIONS
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
Similar Questions
Knowledge Check
- Question 1 - Select One
The sum of the interior angle of a 10-sided polygon is _______
A1260∘B1440∘C1800∘D1620∘ - Question 2 - Select One
Find the sum of the interior angles of the polygon given below .
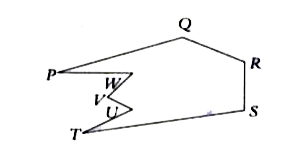 A1080∘B1440∘C1800∘D900∘
A1080∘B1440∘C1800∘D900∘ - Question 3 - Select One
The sum of the interior angle of a 10-sided polygon is _______
A1260∘B1440∘C1800∘D1620∘
Find the sum of the interior angles of the an 8-sided polygon.
View SolutionFind the sum of the interior angles of the an 8-sided polygon.
View SolutionFind the sum of the interior angles of a polygon of 8 sides.
View SolutionFind the sum of the interior angles of the polygon gives below.
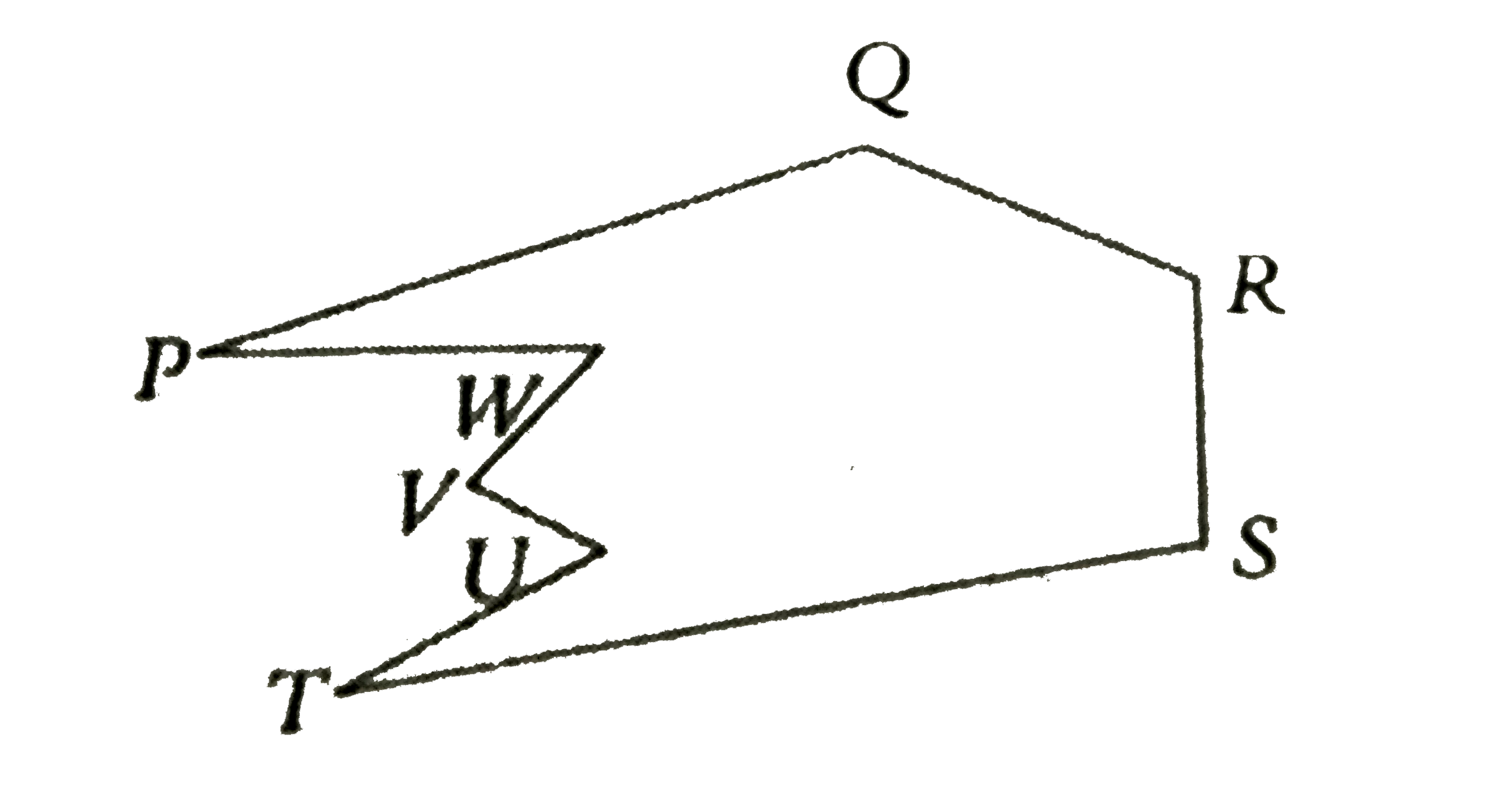 View Solution
View SolutionProve that the sum of the interior angles of an octagon is twice the sum of interior angles of a pentagon
View Solution

