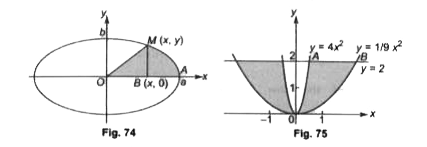
We take on the ellipse
$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b)$
a point M(x,y) lying in the first quadrant.
Show that the sector of the ellipse bonded by its semi-major axis and the focal radius drawn to the point M has an area.
$S = \frac{a b}{2} arc cos \frac{x}{a}$ .
With the aid of this result deduce a formula for computing the area of the entire ellipse.

Text Solution

Verified by Experts

The correct Answer is: $\frac{a b}{4} π$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ is
A $π a b$
B $\frac{π}{4} (a^{2} + b^{2})$
C $π (a + b)$
D $π a^{2} b^{2}$
Question 2 - Select One
The area of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ is
A $π a b$
B $π (a^{2} + b^{2}) / 4$
C $π (a + b)$
DNone
Question 3 - Select One
If the area of the auxiliary circle of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b)$ is twice the area of the ellipse, then the eccentricity of the ellipse is
A $\frac{1}{\sqrt{2}}$
B $\frac{\sqrt{3}}{2}$
C $\frac{1}{\sqrt{3}}$
D $\frac{1}{2}$

IA MARON-APPLICATIONS OF THE DEFINITE INTEGRAL-Computing Areas in Rectangular Coordinates

Home
Ask Doubt
Profile