What is Reciprocal of a function ? explain it by giving an example .
What is Reciprocal of a function and properties?
In this lesson, we will discuss about the idea of reciprocal functions and their general form. We'll look at examples of these types of functions and define their characteristics. We'll also examine how to use these characteristics to graph these types of functions. This would help to get a good understanding of the same and also clear all types of queries without any problem at all.
What Is a Reciprocal Function?
Did you know that the swinging motion of the pendulum can be modeled using mathematical properties and equations? For instance, the frequency (in Hertz), which is the number of full swings per second of one swing of the pendulum, is equal to the reciprocal of the period (in seconds), which is the time it takes for the pendulum to make one full swing back and forth.
Recall that the reciprocal of a number x is 1/x, so, we can find the frequency of a pendulum's swinging motion by finding the reciprocal of the period. For instance, consider a pendulum with a period of 2 seconds. To find the frequency of this pendulum, we find the reciprocal of 2, which is 1/2.
Pretty neat, huh? Let's take it a step further. In general, if we let the frequency of a pendulum be f and the period of a pendulum be p, we have that f = 1/p. In mathematics, we call this a reciprocal function. In the same way that the reciprocal of a number x is 1/x, the reciprocal function of a function f(x) is 1/f(x).

Here, we would consider the function f(x) = 2x - 1. The reciprocal function of f would be as follows:
1/f(x) = 1/(2x - 1)
So far so good! In general, a reciprocal function has the form:
r(x) = a / (x - h) + k
Being familiar with a reciprocal function in this form better allows us to identify various characteristics of the function. Let's consider some of those characteristics.
Reciprocal Function Characteristics
In observing the reciprocal functions characteristics, let's consider the most basic reciprocal function, which is f(x) = 1/x. Take a look at the graph of this function.
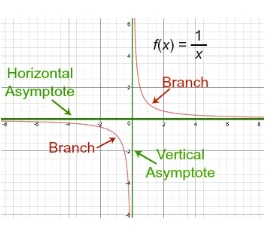
Notice that our graph has two main parts. We call these the branches of the function. Also notice that the function's graph approaches the lines x = 0 and y = 0, but it never actually touches them. We call these lines the asymptotes, which are the horizontal and vertical lines that the graph approaches but doesn't touch. The asymptotes come from the fact that a reciprocal function 1/f(x) must restrict its domain so that the denominator is not equal to 0.
If we're given a reciprocal function in the form 1/f(x), then we can find the vertical asymptotes by setting f(x) = 0 and solving for x. However, when given a reciprocal function in its general form, it's much easier. For the reciprocal function in general form r(x) = a / (x - h) + k, we have the following rules:
- The vertical asymptote of r(x) is x = h.
- The horizontal asymptote of r(x) is y = k.
Well, that's fairly simple! It's just a matter of identifying numbers within the function! The only thing to keep in mind is that the denominator in the general form is x - h, so when identifying the vertical asymptote, x = h, we must keep that negative in mind.
We can use these asymptotes, a few plotted points, and the general shape of the graph to sketch a graph of a reciprocal function. So, being able to identify the asymptotes easily is definitely helpful.


Similar Questions
How to perform Addition subtraction multiplication division on Real function ? Explain by giving example of each.
View SolutionWhat is friction? Explain it with an example.
View SolutionHow to do Multiplication of function by a scalar ? Explain it by giving example
View SolutionWhat do you mean by a precipitation reaction ? Explain by giving examples.
View SolutionWhat is annual range of temperature ?
Explain it by giving one example.View SolutionWhat is Factors Theorem ? (Explain this by giving an example)
View SolutionWhat do you mean by a precipitation reaction? Explain by giving examples.
View SolutionWhat is modulation ? Explain its necessity giving example of size of antenna.
View SolutionWhat do you mean by a precipitation reaction? Explain by giving examples.
View SolutionExplain Reciprocal functions with graph
View Solution


