Which of following functions have the same graph?
f(x)=logeex
g(x)=|x|sgnx
h(x)=cot−1(cotx)
k(x)=limn→∞2|x|πtan−1(nx)
The correct Answer is:A, B, D
To determine which of the given functions have the same graph, we will analyze each function step by step.
Step 1: Analyze the first function f(x)=loge(ex)
1. Domain: The logarithm function requires its argument to be positive. Since ex is always positive for all x, the domain of f(x) is x∈R.
2. Simplification: By properties of logarithms, we can simplify:
f(x)=loge(ex)=x
3. Graph: The graph of f(x)=x is a straight line passing through the origin with a slope of 1.
Step 2: Analyze the second function g(x)=|sgn(x)|x
1. Definition of sgn: The signum function sgn(x) is defined as:
- 1 when x>0
- 0 when x=0
- −1 when x<0
2. Cases:
- When x>0: g(x)=|1|x=x
- When x=0: g(x)=|0|⋅0=0
- When x<0: g(x)=|−1|x=−x (but since we take absolute value, it becomes −(−x)=x)
3. Graph: Thus, g(x)=x for all x. The graph is also a straight line passing through the origin with a slope of 1.
Step 3: Analyze the third function h(x)=cot−1(cot(x))
1. Understanding the function: The function cot−1(cot(x)) is defined for x in the intervals where cot(x) is defined, but it is discontinuous at certain points.
2. Graph: The graph of h(x) does not match the linear graph of f(x) and g(x). It has discontinuities and is not a straight line.
Step 4: Analyze the fourth function k(x)=2xπ for x>0 and −2xπ for x<0
1. Cases:
- When x>0: k(x)=2xπ (as n→∞, this approaches x)
- When x<0: k(x)=−2xπ (as n→∞, this also approaches x)
- When x=0: k(0)=0
2. Graph: Thus, k(x)=x for all x. The graph is also a straight line passing through the origin with a slope of 1.
Conclusion
From the analysis:
- The functions f(x), g(x), and k(x) all simplify to x and have the same graph (a straight line).
- The function h(x) does not match the others.
Final Answer
The functions that have the same graph are:
- f(x)=loge(ex)
- g(x)=|sgn(x)|x
- k(x)=2xπ (for x>0 and x<0)
2. Simplification: By properties of logarithms, we can simplify:
f(x)=loge(ex)=x
3. Graph: The graph of f(x)=x is a straight line passing through the origin with a slope of 1.
- 1 when x>0
- 0 when x=0
- −1 when x<0
2. Cases:
- When x>0: g(x)=|1|x=x
- When x=0: g(x)=|0|⋅0=0
- When x<0: g(x)=|−1|x=−x (but since we take absolute value, it becomes −(−x)=x)
3. Graph: Thus, g(x)=x for all x. The graph is also a straight line passing through the origin with a slope of 1.
2. Graph: The graph of h(x) does not match the linear graph of f(x) and g(x). It has discontinuities and is not a straight line.
- When x>0: k(x)=2xπ (as n→∞, this approaches x)
- When x<0: k(x)=−2xπ (as n→∞, this also approaches x)
- When x=0: k(0)=0
2. Graph: Thus, k(x)=x for all x. The graph is also a straight line passing through the origin with a slope of 1.
- The functions f(x), g(x), and k(x) all simplify to x and have the same graph (a straight line).
- The function h(x) does not match the others.
- f(x)=loge(ex)
- g(x)=|sgn(x)|x
- k(x)=2xπ (for x>0 and x<0)
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 1
5 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 2
6 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Knowledge Check
Which of the following functions have zeros -1, 1, and 4?
Af(x)=(x−4)(1+x2)Bf(x)=(x+4)(1−x2)Cf(x)=(x−1)(x2−3x−4)Df(x)=(x−1)(x2+3x−4)The graph of f(x) is shown below :
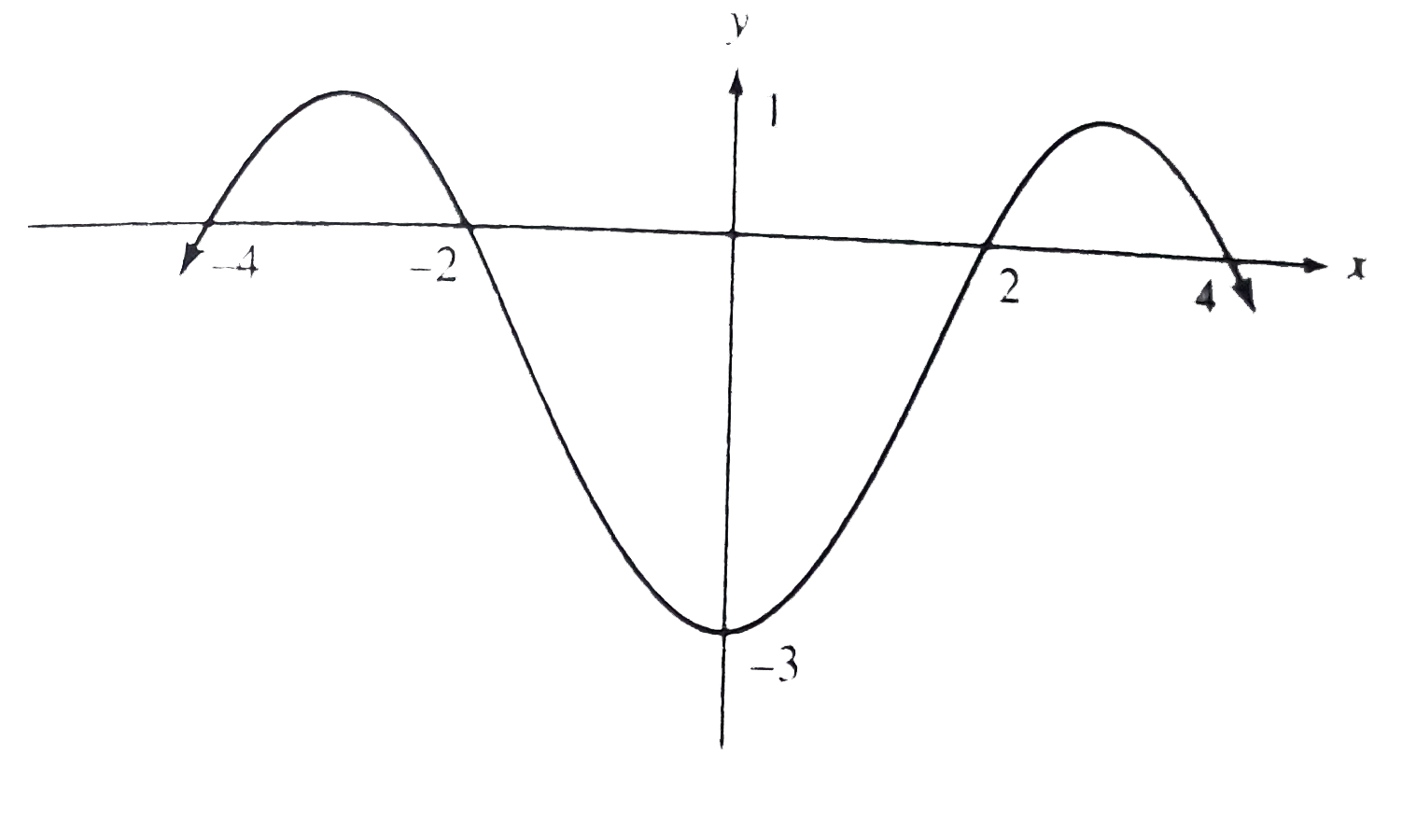
A transformation is applied that results in the following graph :
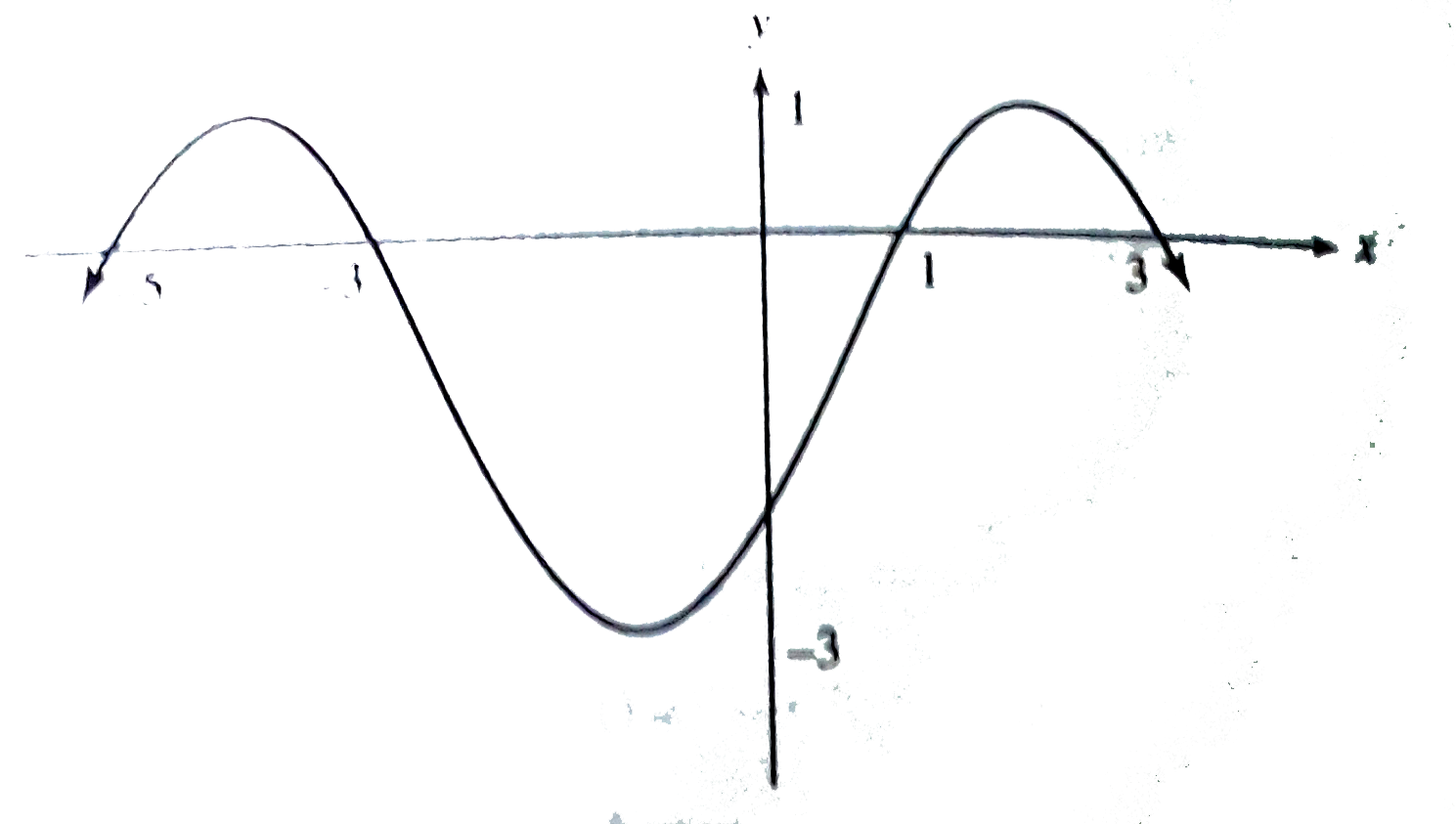
Which of the following functions describes this graph ?Af(x-1)Bf(x+1)Cf(x)-1Df(x)+1
Which of the following species have the same shape?
View SolutionWhich of the following species have the same shape?
View SolutionWhich of the following is a function whose graph is symmetrical about the origin ?
View SolutionWhich of the following pairs have the same number of atoms?
View SolutionWhich of the following pairs have the same dimensions?
View SolutionWhich of the following functions (s) has/have the range equals [-1, 1]?
View Solution
