Which of the following curve is represented by 2x2+6xy+5y2=1?
A
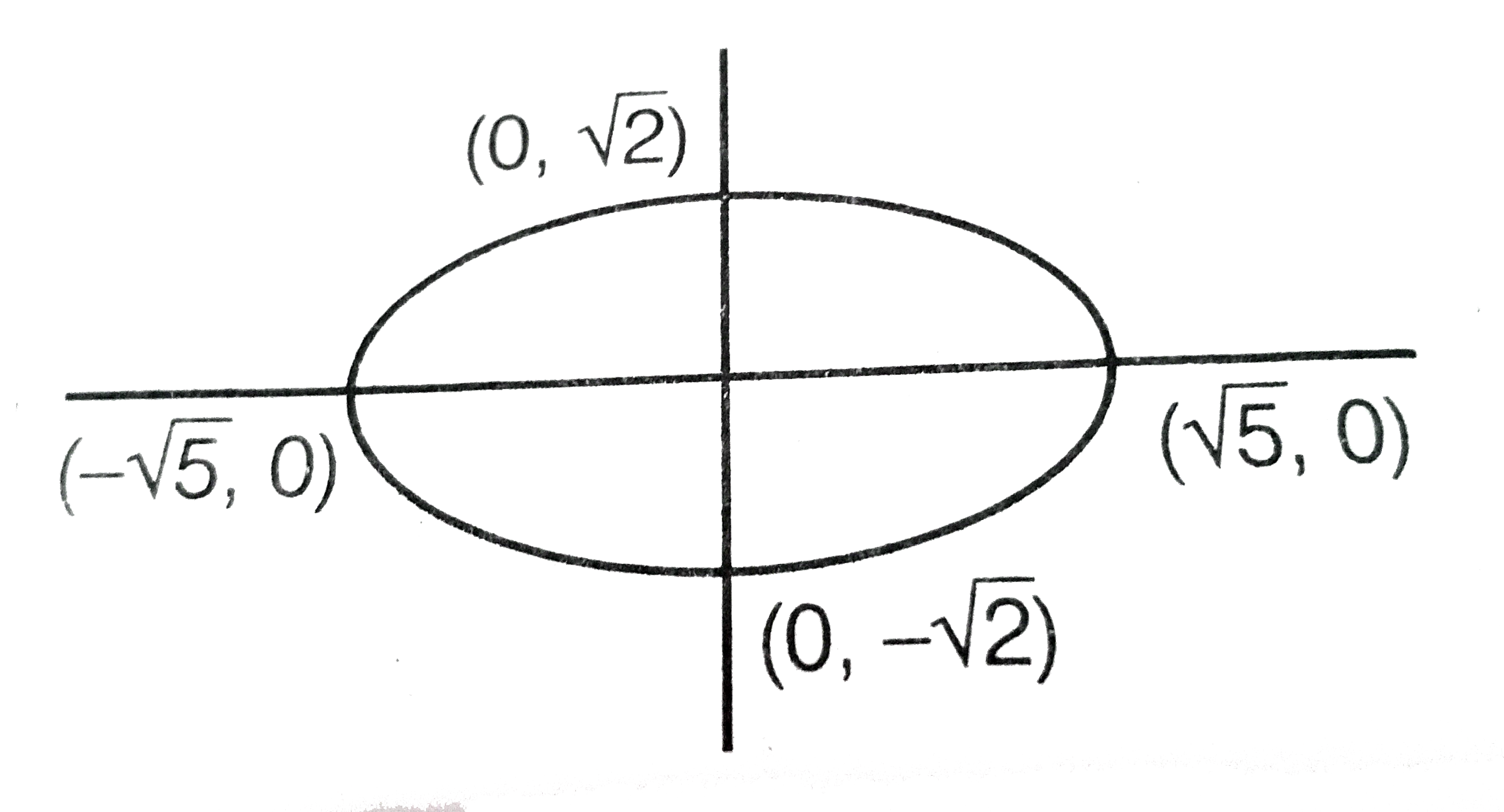
B
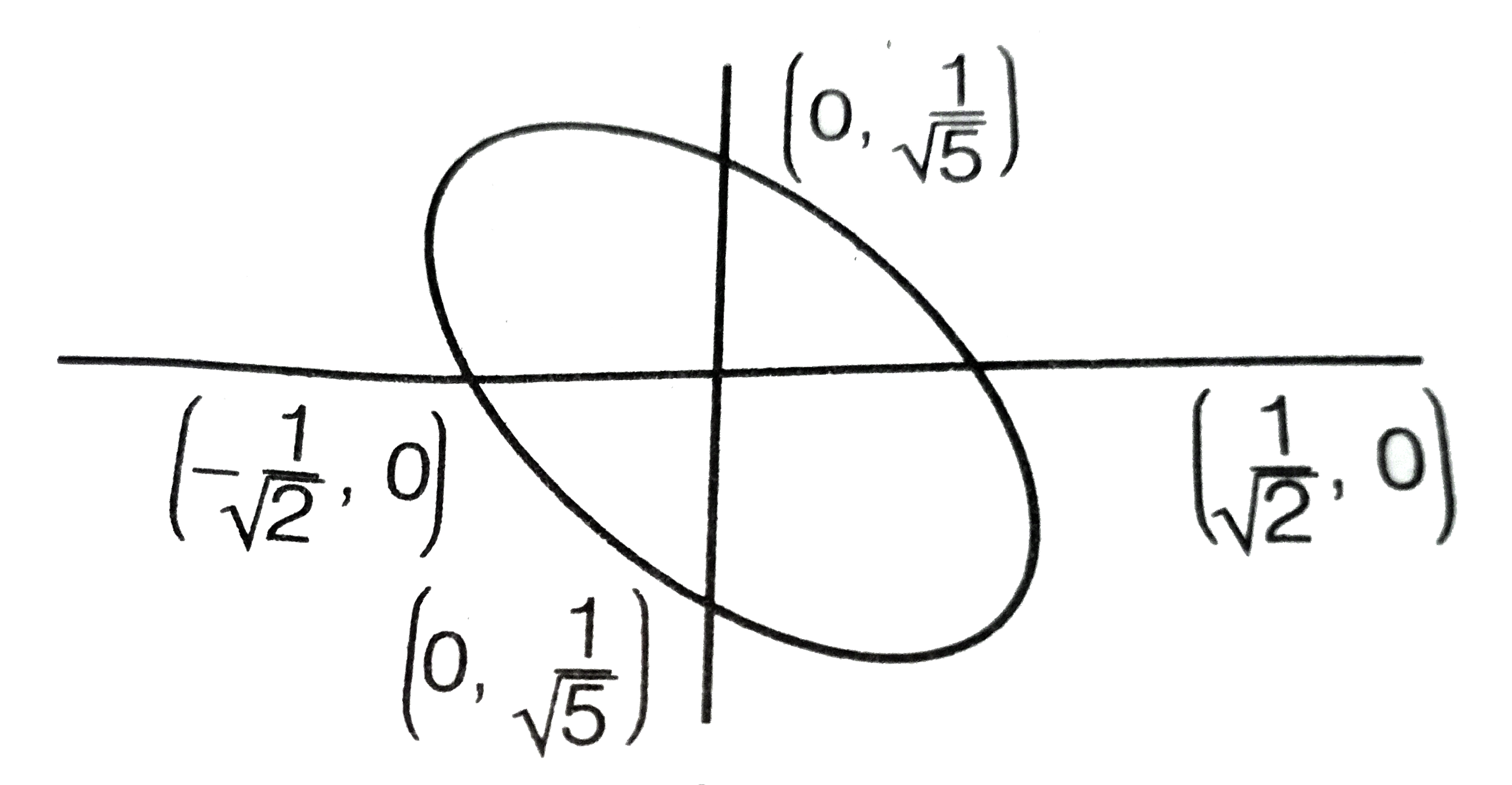
C
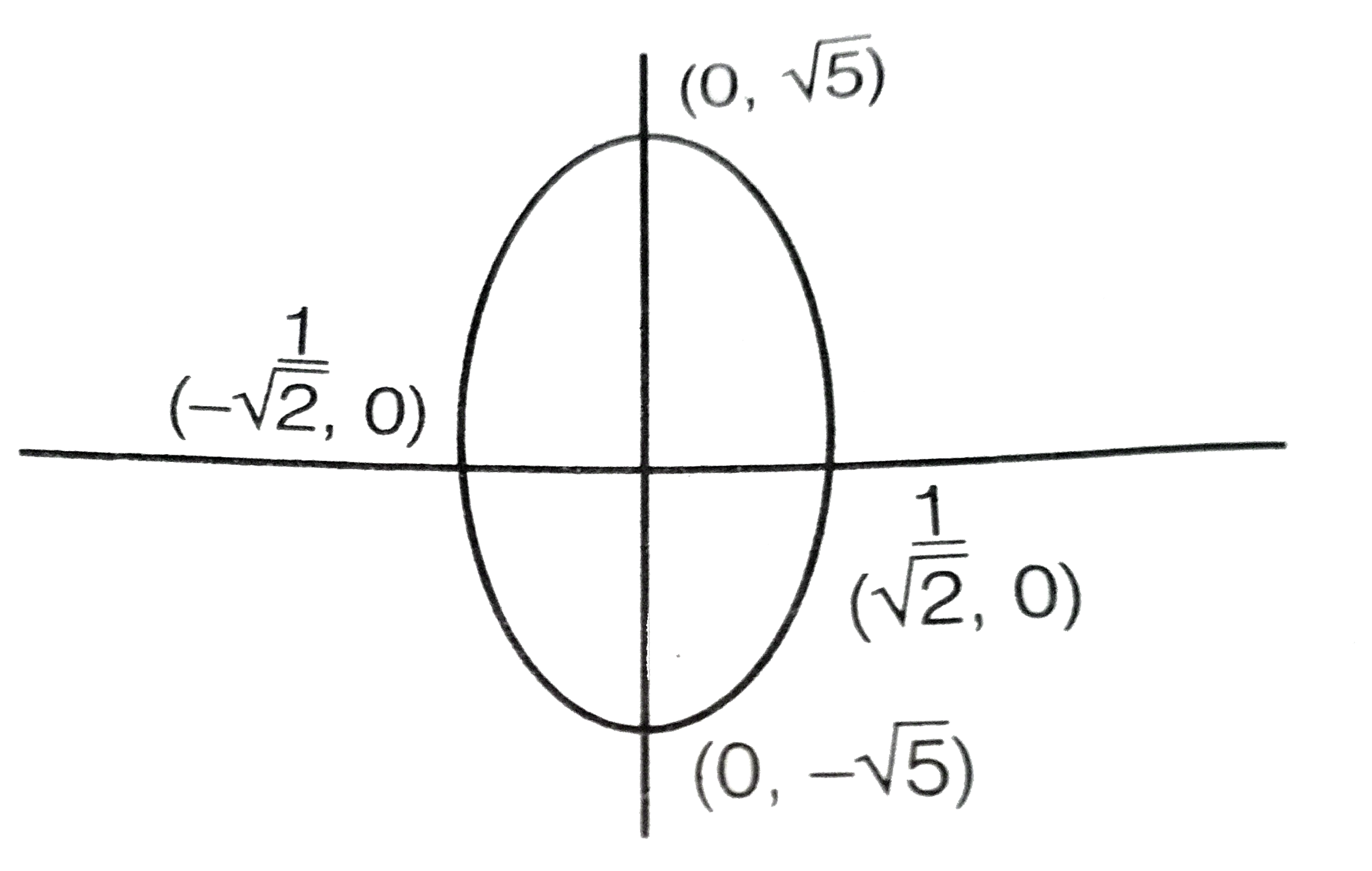
D

Text Solution
The correct Answer is:B
Given equation is
2x2+6xy+5y2=1
By putting - x for x and - y for y, the equation remains same, therefore the curve is symmetric in opposite quadrants.
Putting x=0,5y2=1
⇒y=±1√5
Putting y=0,2x2=1
⇒y=±1√2
Then the curve passes through the points (±1√2,0) and (0,±1√5).
Thus, curve (c ) is the required curve.
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 2
34 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
Which of the following can represent the curve x2=−2y ?
A B
B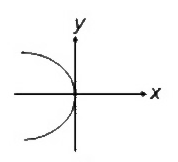 C
C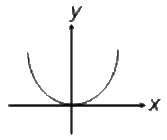 D
D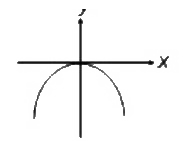
The equation of the lines represented by 6x2−5xy−6y2=0 are
A2x+3y=0and3x+2y=0B2x−3y=0and3x−2y=0C2x−3y=0and3x+2y=0D2x+3y=0and3x−2y=0The acute angle θ between the lines represented by 2x2−6xy+y2=0 is
Atan−1(√72)Btan−1(2√73)Ctan−1(3√72)Dtan−1(2√73)
The product of the perpendiculars from the point (1, 1) to the pair of straight lines represented by 2x2+6xy+3y2=0 is
View SolutionThe Curve represented by the equation 2x2+4xy−2y2+3x+3y+1=0 is
View SolutionThe Curve represented by the equation 2x2+xy+6y2−2x+17y−12=0 is
View Solution2x2+6xy+5y2=1,then
View SolutionThe acute angle between the line represented by x2−6xy+5y2+10x−4y+9=0 is
View Solution
