Which of the following graphs is symmetric about the origin ?
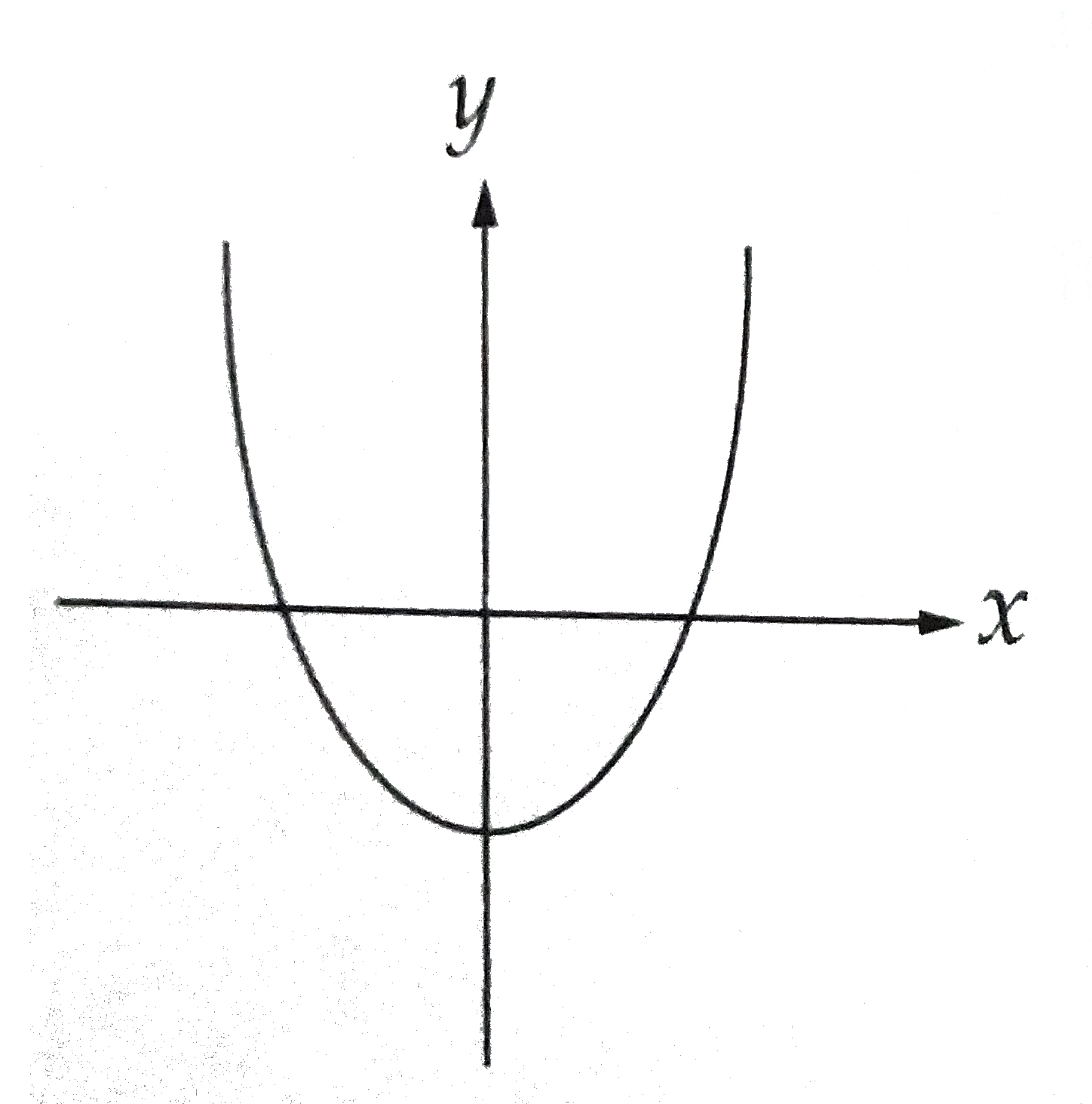



The correct Answer is:D
To determine which of the given graphs is symmetric about the origin, we will analyze each option step by step.
Step 1: Understand Symmetry About the Origin
A graph is symmetric about the origin if rotating it 180 degrees around the origin results in the same graph. Mathematically, this means that if (x, y) is a point on the graph, then (-x, -y) must also be a point on the graph.
Hint: Remember that symmetry about the origin involves flipping both the x and y coordinates.
Step 2: Analyze Each Option
- Option 1: A parabola along the y-axis (e.g., y = x²).
- If we rotate this graph 180 degrees, the graph will look like an inverted parabola (e.g., y = -x²). This does not match the original graph.
Hint: Check if flipping the graph changes its shape or position.
- Option 2: Another parabola along the y-axis (similar to option 1).
- Similar reasoning applies; it will also become inverted and will not match the original graph.
Hint: Look for characteristics of the graph that change upon rotation.
- Option 3: A parabola along the x-axis (e.g., x = y²).
- Rotating this graph 180 degrees will also result in an inverted graph (e.g., x = -y²), which does not match the original.
Hint: Consider how the orientation of the graph changes with rotation.
- Option 4: A rectangular hyperbola in the first and second quadrants.
- When this graph is rotated 180 degrees, it will change its shape and orientation, resulting in a different graph.
Hint: Visualize how the hyperbola would look after rotation.
- Option 5: A rectangular hyperbola in the first and third quadrants.
- When this graph is rotated 180 degrees, it remains unchanged. The points (x, y) become (-x, -y), and the shape stays the same.
Hint: Check if the graph looks identical after a 180-degree rotation.
Step 3: Conclusion
After analyzing all options, we find that Option 5 is the only graph that is symmetric about the origin.
Final Answer: The graph that is symmetric about the origin is Option 5.
A graph is symmetric about the origin if rotating it 180 degrees around the origin results in the same graph. Mathematically, this means that if (x, y) is a point on the graph, then (-x, -y) must also be a point on the graph.
- Option 1: A parabola along the y-axis (e.g., y = x²).
- If we rotate this graph 180 degrees, the graph will look like an inverted parabola (e.g., y = -x²). This does not match the original graph.
Hint: Check if flipping the graph changes its shape or position.
- Similar reasoning applies; it will also become inverted and will not match the original graph.
- Rotating this graph 180 degrees will also result in an inverted graph (e.g., x = -y²), which does not match the original.
- When this graph is rotated 180 degrees, it will change its shape and orientation, resulting in a different graph.
- When this graph is rotated 180 degrees, it remains unchanged. The points (x, y) become (-x, -y), and the shape stays the same.
After analyzing all options, we find that Option 5 is the only graph that is symmetric about the origin.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following shapes is not symmetrical about the horizontal line ?
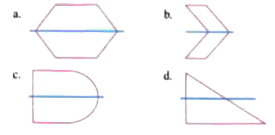 .AABBCCDD
.AABBCCDDWhich of the following shapes is not symmetrical about the vertical line ?
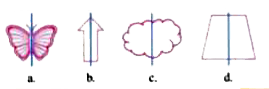 AABBCCDD
AABBCCDDWhich of the following graphs is NOT a function ?
A B
B C
C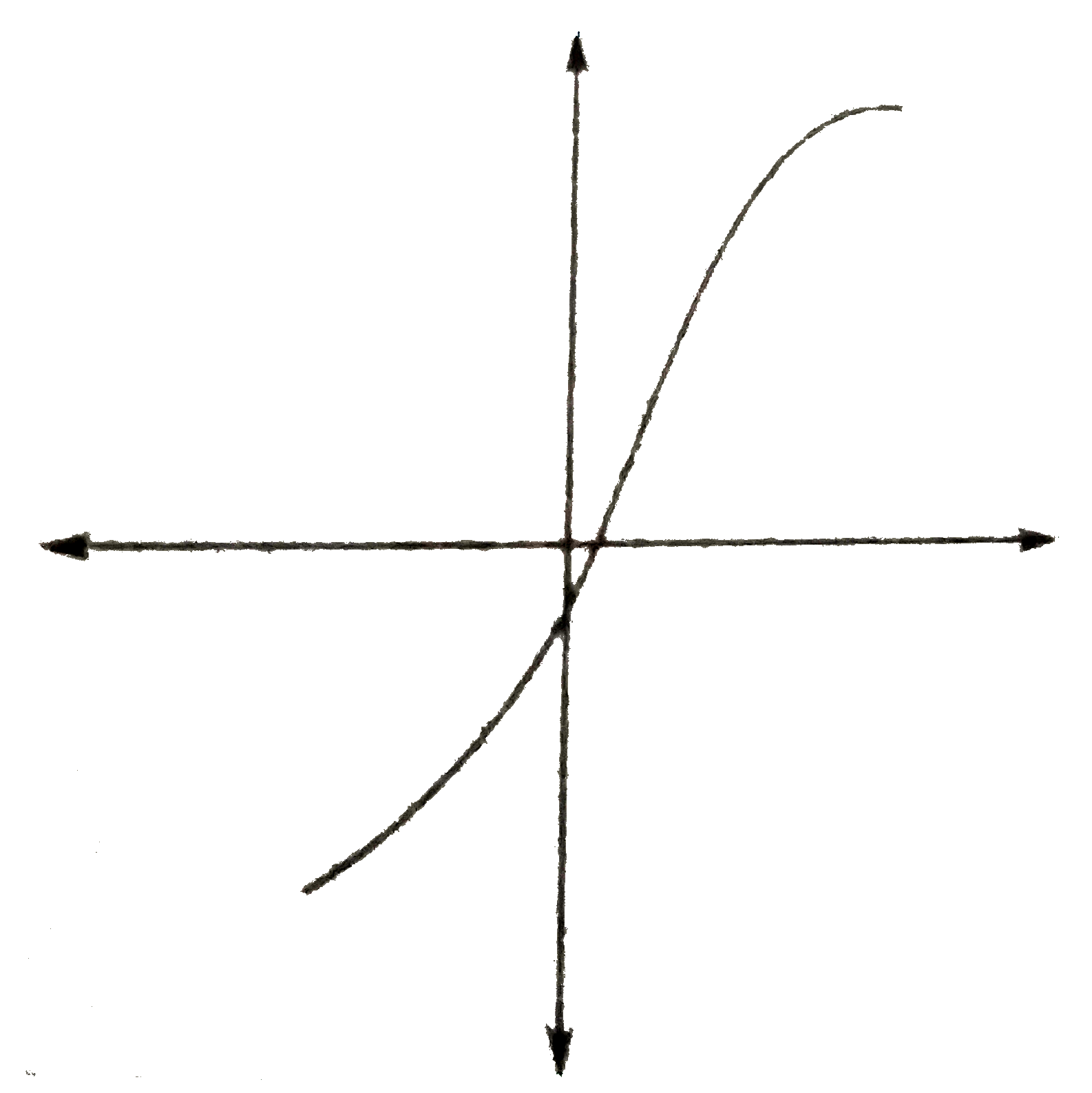 D
D
Which of the following is a function whose graph is symmetrical about the origin ?
View SolutionLet A be a square matrix. Then which of the following is not a symmetric matrix -
View SolutionA rhombus is symmetrical about
View SolutionWhich of the following statements is true about the graph of the equation 2y − 3x = −4 in the xy-plane?
View SolutionWhich of the following is incorrect about the given graph ?
View Solution