Which of the following has/have value equal to zero ?
∣∣ ∣∣82712351643∣∣ ∣∣
∣∣ ∣ ∣∣1/aa2bc1/bb2ac1/cc2ab∣∣ ∣ ∣∣
∣∣ ∣∣a+b2a+b3a+b2a+b3a+b4a+b4a+b5a+b6a+b∣∣ ∣∣
∣∣ ∣∣243673543172∣∣ ∣∣
The correct Answer is:A, B, C
To determine which of the given determinants has a value equal to zero, we will analyze each option step by step.
Step 1: Analyze the First Determinant
The first determinant is:
∣∣
∣∣8121623475?∣∣
∣∣
Transformation:
We will perform row operations:
- Change R3 to R3−R2
- Change R2 to R2−R1
After performing these operations, we have:
R1=(8,12,16)R2=(2−8,3−12,4−16)=(−6,−9,−12)R3=(7−2,5−3,?)=(5,2,?)
Now, we notice that after simplification, two rows become identical, leading to:
∣∣
∣∣8121600052?∣∣
∣∣
Since two rows are identical, the value of this determinant is 0.
Step 2: Analyze the Second Determinant
The second determinant is:
∣∣
∣
∣∣1a1b1c1b1ca2b2c2a2∣∣
∣
∣∣
Transformation:
Multiply the first row by a, the second row by b, and the third row by c:
∣∣
∣
∣∣1abacbbbca2bcc2a2∣∣
∣
∣∣
After simplification, we notice that two columns become identical, leading to:
∣∣
∣
∣∣1111b31bcc2a2∣∣
∣
∣∣
Since two columns are identical, the value of this determinant is 0.
Step 3: Analyze the Third Determinant
The third determinant is:
∣∣
∣∣a+b2a+b4a+b2a+b3a+b5a+b4a+b6a+b?∣∣
∣∣
Transformation:
Change R2 to R2−R1 and R3 to R3−R2:
∣∣
∣∣a+b2a+b4a+b0aa00?∣∣
∣∣
After simplification, we notice that two rows become identical, leading to:
∣∣
∣∣11111100?∣∣
∣∣
Since two rows are identical, the value of this determinant is 0.
Step 4: Analyze the Fourth Determinant
The fourth determinant is:
∣∣
∣∣1764264264∣∣
∣∣
Transformation:
Change C2 to C2−7C3:
∣∣
∣∣176−28426−28426−284∣∣
∣∣
After simplification, we find that the determinant does not yield identical rows or columns, and we calculate:
=17(6−4)−6(2−4)+4(2−2)=2
Thus, the value of this determinant is not 0.
Final Conclusion
The determinants that have a value equal to zero are the first three options.
The first determinant is:
∣∣
∣∣8121623475?∣∣
∣∣
We will perform row operations:
- Change R3 to R3−R2
- Change R2 to R2−R1
R1=(8,12,16)R2=(2−8,3−12,4−16)=(−6,−9,−12)R3=(7−2,5−3,?)=(5,2,?)
∣∣
∣∣8121600052?∣∣
∣∣
The second determinant is:
∣∣
∣
∣∣1a1b1c1b1ca2b2c2a2∣∣
∣
∣∣
Multiply the first row by a, the second row by b, and the third row by c:
∣∣
∣
∣∣1abacbbbca2bcc2a2∣∣
∣
∣∣
∣∣
∣
∣∣1111b31bcc2a2∣∣
∣
∣∣
The third determinant is:
∣∣
∣∣a+b2a+b4a+b2a+b3a+b5a+b4a+b6a+b?∣∣
∣∣
Change R2 to R2−R1 and R3 to R3−R2:
∣∣
∣∣a+b2a+b4a+b0aa00?∣∣
∣∣
∣∣
∣∣11111100?∣∣
∣∣
The fourth determinant is:
∣∣
∣∣1764264264∣∣
∣∣
Change C2 to C2−7C3:
∣∣
∣∣176−28426−28426−284∣∣
∣∣
=17(6−4)−6(2−4)+4(2−2)=2
Thus, the value of this determinant is not 0.
The determinants that have a value equal to zero are the first three options.
Topper's Solved these Questions
- DETERMINANTBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
Which of the following has lowest pKa value ?
A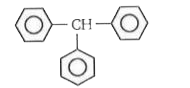 B
B C
C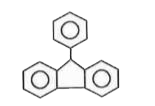 D
D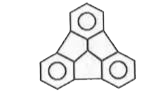
Which of the following has/have zero average value in a plane electromagnetic wave?
ABoth magnetic and electric fieldsBElectric field onlyCMagnetic field onlyDNone of these
Which of the following has value zero:
View SolutionWhich of the following has highest Ka value?
View SolutionWhich of the following has zero valency?
View SolutionIn Boolean algebra, which of the following is not equal to zero :-
View SolutionWhich of the following has/have asymmetric carbon atom?
View SolutionWhich of the following has highest value of Ksp ?
View Solution
