Which of the following is/are true about the ellipse x2+4y2−2x−16y+13=0? (a)the latus rectum of the ellipse is 1. (b)The distance between the foci of the ellipse is 4√3. (c)The sum of the focal distances of a point P(x,y) on the ellipse is 4. (d)Line y=3 meets the tangents drawn at the vertices of the ellipse at points P and Q . Then PQ subtends a right angle at any of its foci.Solution in Bengali
The latus rectum of the ellipse is 1
The distance between the foci of the ellipse is 4√3
The sum of the focal distances of a point P(x,y) on the ellipse is 4
Liney=3 meets the tangents drawn at the vertices of the ellipse at points P and Q. Then PQ subtends a right angle at any of its foci.
x2+4y2−2x−16y+13=0
or (x2−2x+1)+4(y2−4y+4)=4
or (x−1)24+(y−2)21=1
∴ Length of latus rectum =2×12=1
Also, e=√1−14=√34
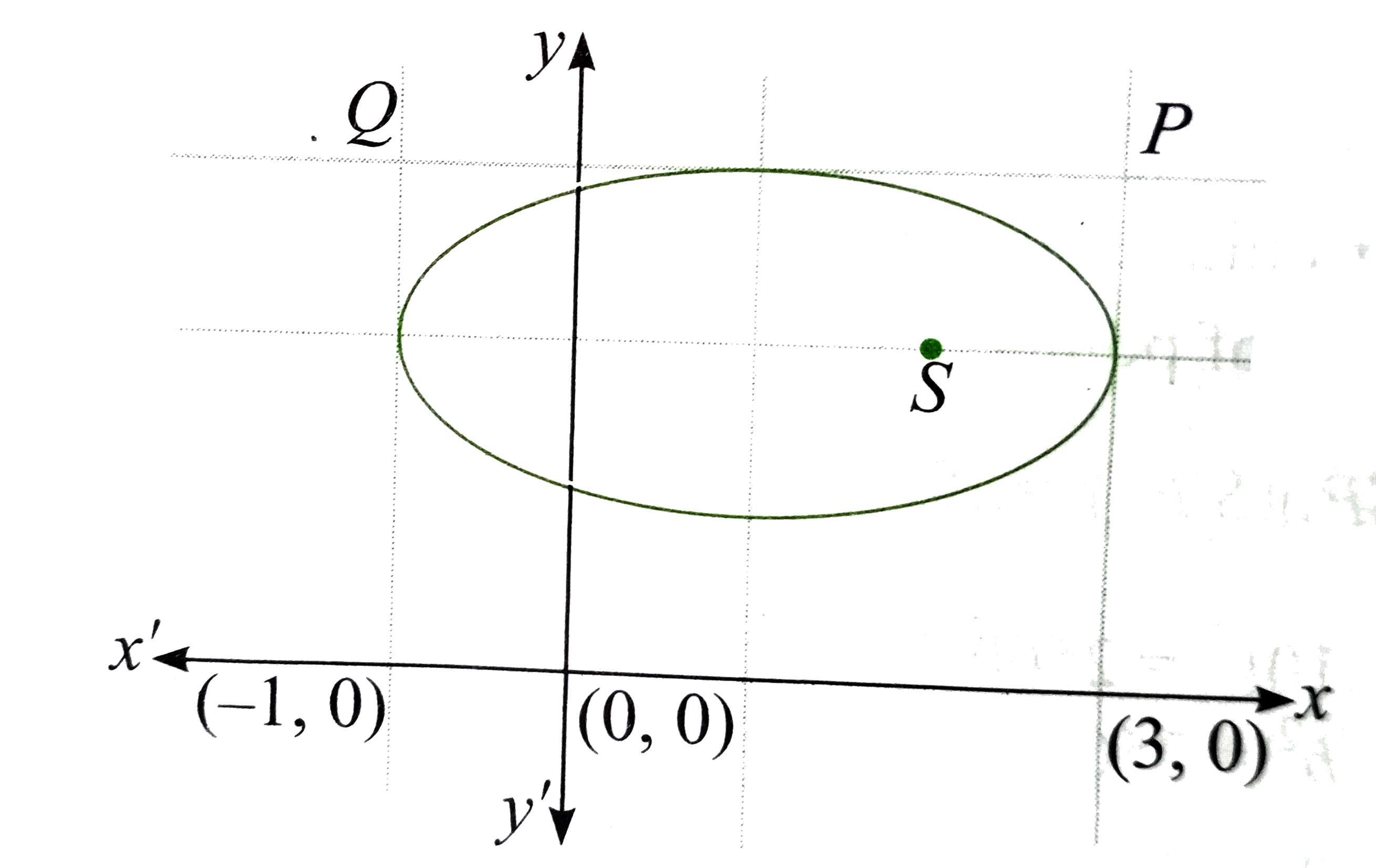
or 2ae=2×2×√32=√3
Sum of the focal distance =2a=4
Tenagents at the vertices are
x−1=±2
or x=3,−1
Therefore the line y=3 intersects these at points P(3,3) and Q(-1,3)
One of the foci is S(√3+1,2)
Slop of PS=12−√3
Slopo of QS=1−2−√3
∴ Product of slops =12−√3×1−2−√3=−1
Similar Questions
Which of the following is/are true about the ellipse x2+4y2−2x−16y+13=0? (a)the latus rectum of the ellipse is 1. (b)The distance between the foci of the ellipse is 4√3. (c)The sum of the focal distances of a point P(x,y) on the ellipse is 4. (d)Line y=3 meets the tangents drawn at the vertices of the ellipse at points P and Q . Then PQ subtends a right angle at any of its foci.
05:02View SolutionColumn I, Column II An ellipse passing through the origin has its foci (3, 4) and (6,8). Then the length of its minor axis is, p. 8 If PQ is a focal chord of the ellipse x225+y216=1 which passes through S≡(3,0) and PS=2, then the length of chord PQ is, q. 10√2 If the line y=x+K touches the ellipse 9x2+16y2=144, then the difference of values of K is, r. 10 The sum of distances of a point on the ellipse x29+y216=1 from the foci is, s. 12
10:00View SolutionEllipse x^2 +4y^2 =4 One touch line ellipse x^2+2y^2= 6 Meets at P and Q. Prove that ellipse x^2+y^2 = 6 The tangent lines drawn at P and Q are at right angles.
12:59View Solutionदीर्घवृत्त x2+4y2=4 की स्पर्श रेखा, दीर्घवृत्त x2+2y2=6 को P व Q बिन्दुओं पर मिलती है। सिद्ध कीजिए कि P व Q पर दीर्घवृत्त x2+2y2=6 की स्पर्श रेखायें लम्बवत् होंगी।
10:39View SolutionA tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P&Q. The angle between the tangents at P and Q of the ellipse x 2 +2y 2 =6 is
05:32View SolutionThe vertices of the triangle ABC are A(0,0),B(3,0)andC(3,4), where A and C are foci of an ellipse and B lies on the ellipse. If the length of the latus rectum of the ellipse is 12p units, then the vlaue of p is
03:10View SolutionWhich of the following is/are true about the ellipse x2+4y2−2x−16y+13=0? the latus rectum of the ellipse is 1. The distance between the foci of the ellipse is 4√3. The sum of the focal distances of a point P(x,y) on the ellipse is 4. Line y=3 meets the tangents drawn at the vertices of the ellipse at points P and Q . Then PQ subtends a right angle at any of its foci.
04:20View SolutionColumn I, Column II An ellipse passing through the origin has its foci (3, 4) and (6,8). Then the length of its minor axis is, p. 8 If P Q is a focal chord of the ellipse (x^2)/(25)+(y^2)/(16)=1 which passes through S-=(3,0) and P S=2, then the length of chord P Q is, q. 10sqrt(2) If the line y=x+K touches the ellipse 9x^2+16 y^2=144 , then the difference of values of K is, r. 10 The sum of distances of a point on the ellipse (x^2)/9+(y^2)/(16)=1 from the foci is, s. 12
04:48View Solution

