Which of the following is not a Euclid's axiom?
The whole is greater than the part
Things which are double of the same things are equal to one another.
Thing which are halves of the same things are equal to one another.
If two things are equal, then their sum is equal to of the one thing.
The correct Answer is:D
To determine which of the following statements is not a Euclid's axiom, we will analyze each option one by one.
1. Option A: The whole is greater than the part.
- This statement is true and is indeed one of Euclid's axioms. It states that if you have a whole, it must be greater than any of its parts. Therefore, this option is not the answer.
2. Option B: Things which are double of the same thing are equal to one another.
- This statement is also true and corresponds to Euclid's axiom. If A and B are both double of C, then A = B. Thus, this option is not the answer.
3. Option C: Things which are half of the same thing are equal to one another.
- This statement is true as well. If A and B are both half of C, then A = B. Therefore, this option is also not the answer.
4. Option D: If two things are equal, then their sum is equal to one third of one thing.
- This statement is not true. If A = B, then A + B = 2A, not one third of one thing. This does not align with Euclid's axioms, making this option the correct answer.
Conclusion:
The statement that is not a Euclid's axiom is Option D: "If two things are equal, then their sum is equal to one third of one thing."
---
- This statement is true and is indeed one of Euclid's axioms. It states that if you have a whole, it must be greater than any of its parts. Therefore, this option is not the answer.
- This statement is also true and corresponds to Euclid's axiom. If A and B are both double of C, then A = B. Thus, this option is not the answer.
- This statement is true as well. If A and B are both half of C, then A = B. Therefore, this option is also not the answer.
- This statement is not true. If A = B, then A + B = 2A, not one third of one thing. This does not align with Euclid's axioms, making this option the correct answer.
The statement that is not a Euclid's axiom is Option D: "If two things are equal, then their sum is equal to one third of one thing."
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Achievers Section (HOTS)3videos
INTRODUCTION TO EUCLID'S GEOMETRY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET B 2019EXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER SET B 2019
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - ACHIEVERS SECTION (HOTS)2videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
Knowledge Check
- Question 1 - Select One
Euclid was-
AGreek MathematicianBContributor to the use of deductive principles of logic as the basis of geometryCPropounded the geometrical theoremDAll of these - Question 2 - Select One
Read the following statements:
A. Axioms are propositions which are assumed.
B. Axioms are special theorems.
C. Axioms are definitions.
D. Axioms, when proved becomes theorems.
Which of the following statement(s) is correct?AOnly ABA and CCA and DDOnly B - Question 3 - Select One
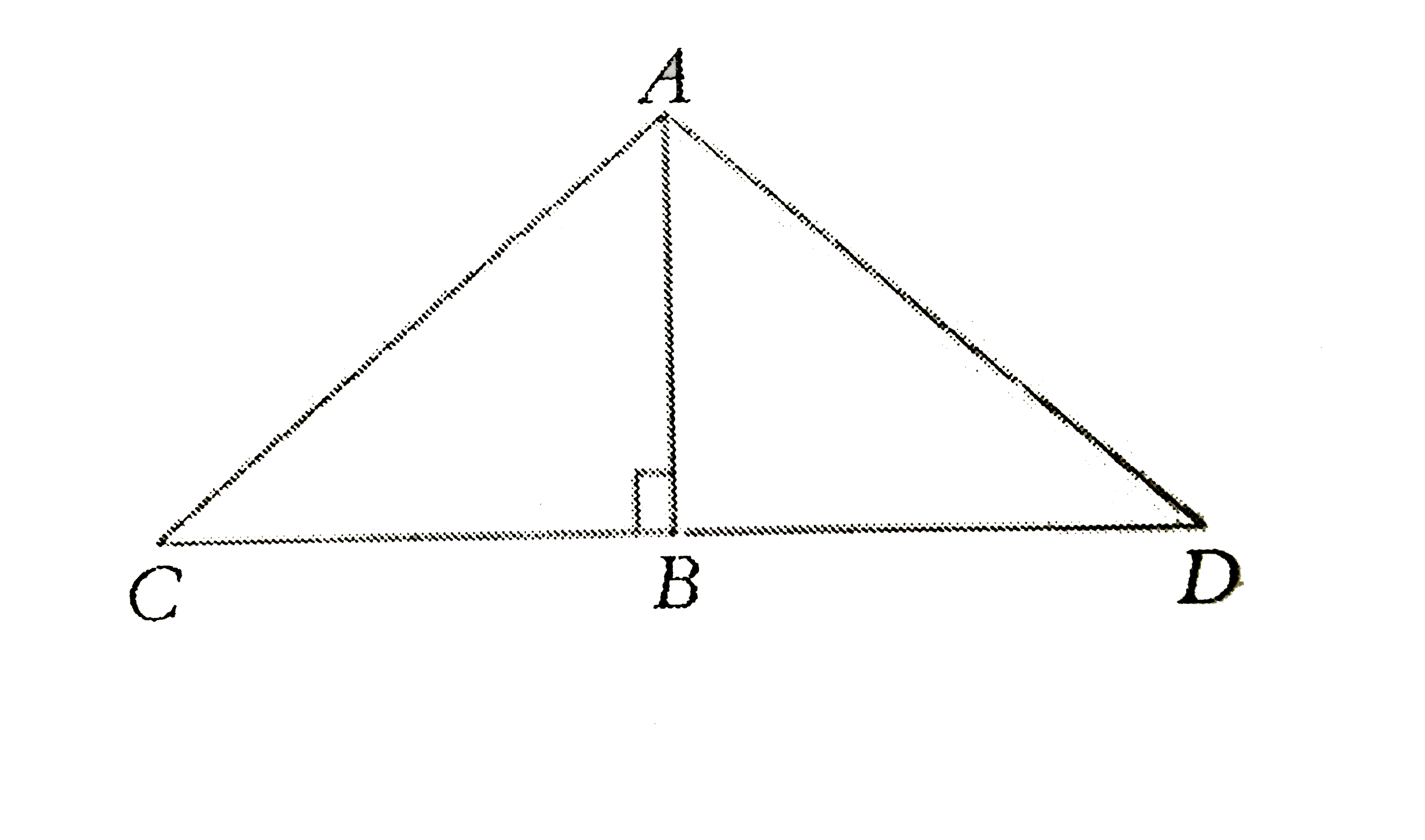
In the figure above ,AB is the perpendicular bisector of CD. Which of the following axioms best proves the congurence of ΔABCandΔABD ?ASSSBSASCRHSDASA

In the figure above ,AB is the perpendicular bisector of CD. Which of the following axioms best proves the congurence of ΔABCandΔABD ?View SolutionWhy is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
View SolutionIntroduction and Euclid's Axioms
View SolutionWe have AC=XD , C is the mid point of AB and D is the mid point of XY, Using Euclid's axiom ,show that AB=XY
View SolutionA is of the same age as B and C is of the same age as B Euclid 's which axiom illustrates the relative ages of A and C?
View Solution

