Which of the following is the least? sin 3 (b) sin 2 (c) sin 1 (d) sin 7

A

sin 3

B

sin 2

C

sin 1

D

sin 7

Text Solution

Verified by Experts

The correct Answer is:D

(d) $sin 3 = sin [π - (π - 3)] = sin (π - 3) = sin (0.14)$
$sin 2 = sin [π - (π - 2)] = sin (π - 2) = sin (1.14)$
$sin 7 = sin [2 π - (7 - 2 π)] = sin (7 - 2 π) = sin (0.72)$
Now, $1.14 > 1 > 0.72 > 0.14$
$\Rightarrow sin (1.14) > sin 1 > sin (0.72) > sin (0.14)$
[as 1.14,1,0.72, 0.14 lie in the first quadrant and sine functions increase in the first quadrant]
Hence, among the given values, sin3 is the least.
Alternate solution:
We draw the graph of $y = sin x$ abd compare the height of graph for different angles.

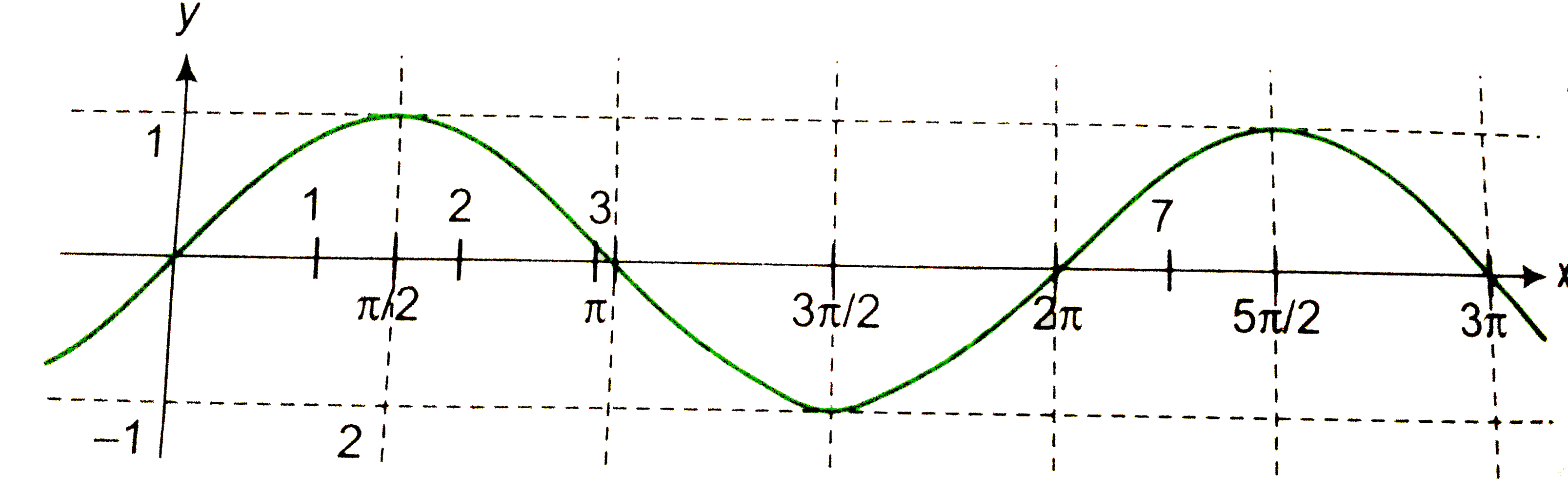
Form the graph, clearly sin 3 is the least as height of graph is the least for angle '3' radians.

Updated on:21/07/2023

|

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the line $x = y = z$ intersects the line
$x sin A + y sin B + z sin C = 2 d^{2}$
$x sin 2 A + y sin 2 B + z sin 2 C = d^{2}$
where $A + B + C = π$ , then $sin \frac{A}{2} sin \frac{B}{2} sin \frac{C}{2} =$
A $\frac{1}{8}$
B $\frac{1}{12}$
C $\frac{1}{16}$
D $\frac{1}{32}$
If A, B and C are the angles of a triangle and
$∣ ∣ ∣ ∣ ∣ \begin{matrix} 1 & 1 & 1 1 + sin A & 1 + sin B & 1 + sin C sin A + {sin}^{2} A & sin B + {sin}^{2} B & sin C + {sin}^{2} C \end{matrix} ∣ ∣ ∣ ∣ ∣ = 0$ , then the triangle ABC is
Aisosceles
Bequilateral
Cright angled isosceles
Dnone of these

CENGAGE-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE

Home
Ask Doubt
Profile