Which of the rational numbers −1128,−57,9−14,29−42 is the greatest?
−1128
−57
9−14
29−42
To determine which of the rational numbers −1128, −57, 9−14, and 29−42 is the greatest, we will follow these steps:
Step 1: Convert all rational numbers to have a common denominator
To compare these fractions easily, we need to find a common denominator. The denominators are 28, 7, -14, and -42.
The least common multiple (LCM) of these denominators can be calculated as follows:
- The factors of 28 are 22×7.
- The factors of 7 are 71.
- The factors of -14 are 21×71.
- The factors of -42 are 21×31×71.
Taking the highest power of each prime factor:
- For 2, the highest power is 22 from 28.
- For 3, the highest power is 31 from -42.
- For 7, the highest power is 71.
Thus, the LCM is:
LCM=22×31×71=4×3×7=84.
Step 2: Convert each fraction to have the common denominator of 84
Now, we will convert each fraction to have a denominator of 84:
1. For −1128:
−1128=−11×328×3=−3384.
2. For −57:
−57=−5×127×12=−6084.
3. For 9−14:
9−14=−9×614×6=−5484.
4. For 29−42:
29−42=−29×242×2=−5884.
Step 3: Compare the numerators
Now we have the following fractions with a common denominator:
- −3384
- −6084
- −5484
- −5884
To determine which is the greatest, we compare the numerators:
- −33
- −60
- −54
- −58
Since all these numbers are negative, the one with the least absolute value is the greatest.
Step 4: Identify the greatest rational number
Among the numerators:
- −33 (from −1128)
- −60 (from −57)
- −54 (from 9−14)
- −58 (from 29−42)
The greatest (least negative) is −33.
Conclusion
Thus, the greatest rational number among the given options is:
−1128.
To compare these fractions easily, we need to find a common denominator. The denominators are 28, 7, -14, and -42.
- The factors of 28 are 22×7.
- The factors of 7 are 71.
- The factors of -14 are 21×71.
- The factors of -42 are 21×31×71.
- For 2, the highest power is 22 from 28.
- For 3, the highest power is 31 from -42.
- For 7, the highest power is 71.
LCM=22×31×71=4×3×7=84.
Now, we will convert each fraction to have a denominator of 84:
−1128=−11×328×3=−3384.
−57=−5×127×12=−6084.
9−14=−9×614×6=−5484.
29−42=−29×242×2=−5884.
Now we have the following fractions with a common denominator:
- −3384
- −6084
- −5484
- −5884
- −33
- −60
- −54
- −58
Among the numerators:
- −33 (from −1128)
- −60 (from −57)
- −54 (from 9−14)
- −58 (from 29−42)
Thus, the greatest rational number among the given options is:
−1128.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIONAL NUMBERS EXERCISE - Exercise (Match the Following)2videos
RATIONAL NUMBERS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIONAL NUMBERS EXERCISE - Exercise (Assertion & Reason Type)5videos
RATIONAL NUMBERS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIONAL NUMBERS EXERCISE - Exercise (Multiple Choice Questions) (LEVEl-1)35videos
RATIONAL NUMBERS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PRACTICAL GEOMETRYEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS LEVEL-2)33videos
PRACTICAL GEOMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - Olympiad/HOTS Corner20videos
SQUARES AND SQUARE ROOTS
Similar Questions
Knowledge Check
- Question 1 - Select One
A rational number between 57 and 911 is .
A5977B3177C2311D79 - Question 2 - Select One
Which number line correctly shows the rational number (97÷2414) ?
A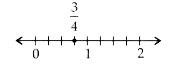 B
B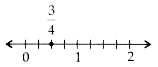 C
C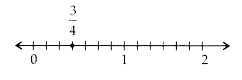 D
D
What per cent is the least rational number of the greatest rational number, if 12,25,13 and 59 are arranged in ascending order?
View SolutionFind 10 rational numbers between −211and911.
View SolutionWrite the additive inverse of each of the following rational numbers:
(i)49
(ii)−137
(iii)5−11
(iv)−11−14View Solution37+(−514)+(−1114)
View SolutionWhich of the following rational numbers are equal? −721 and3−9 (ii) −8−14 and1321
View SolutionWhich of the pair represent the same rational number ?
−5−9and5−9View Solution
