Write down the truth table for the statement
(~p∨q)∧(~p∧~q)
To construct the truth table for the statement (∼p∨q)∧(∼p∧∼q), we will follow these steps:
Step 1: Identify the variables
The variables in our statement are p and q. Each variable can take two values: True (T) or False (F).
Step 2: Create a truth table structure
We will create a truth table with columns for p, q, ∼p, ∼q, ∼p∨q, ∼p∧∼q, and finally (∼p∨q)∧(∼p∧∼q).
Step 3: Fill in the truth values for p and q
We will list all possible combinations of truth values for p and q:
- p=T,q=T
- p=T,q=F
- p=F,q=T
- p=F,q=F
Step 4: Calculate ∼p and ∼q
For each combination of p and q, we will compute ∼p (not p) and ∼q (not q):
- If p=T, then ∼p=F
- If p=F, then ∼p=T
- If q=T, then ∼q=F
- If q=F, then ∼q=T
Step 5: Calculate ∼p∨q
Now we will compute ∼p∨q (not p or q):
- This expression is true if at least one of ∼p or q is true.
Step 6: Calculate ∼p∧∼q
Next, we will compute ∼p∧∼q (not p and not q):
- This expression is true only if both ∼p and ∼q are true.
Step 7: Calculate the final expression
Finally, we will compute (∼p∨q)∧(∼p∧∼q):
- This expression is true only if both ∼p∨q and ∼p∧∼q are true.
Step 8: Complete the truth table
Now, we can fill in the truth table with the calculated values.
| p | q | ∼p | ∼q | ∼p∨q | ∼p∧∼q | (∼p∨q)∧(∼p∧∼q) |
|---------|---------|---------------|---------------|----------------------|----------------------------|-----------------------------------------------------|
| T | T | F | F | T | F | F |
| T | F | F | T | F | F | F |
| F | T | T | F | T | F | F |
| F | F | T | T | T | T | T |
Final Result
The final column (∼p∨q)∧(∼p∧∼q) shows the overall truth values for the given statement.
The variables in our statement are p and q. Each variable can take two values: True (T) or False (F).
We will create a truth table with columns for p, q, ∼p, ∼q, ∼p∨q, ∼p∧∼q, and finally (∼p∨q)∧(∼p∧∼q).
We will list all possible combinations of truth values for p and q:
- p=T,q=T
- p=T,q=F
- p=F,q=T
- p=F,q=F
For each combination of p and q, we will compute ∼p (not p) and ∼q (not q):
- If p=T, then ∼p=F
- If p=F, then ∼p=T
- If q=T, then ∼q=F
- If q=F, then ∼q=T
Now we will compute ∼p∨q (not p or q):
- This expression is true if at least one of ∼p or q is true.
Next, we will compute ∼p∧∼q (not p and not q):
- This expression is true only if both ∼p and ∼q are true.
Finally, we will compute (∼p∨q)∧(∼p∧∼q):
- This expression is true only if both ∼p∨q and ∼p∧∼q are true.
Now, we can fill in the truth table with the calculated values.
|---------|---------|---------------|---------------|----------------------|----------------------------|-----------------------------------------------------|
| T | T | F | F | T | F | F |
| T | F | F | T | F | F | F |
| F | T | T | F | T | F | F |
| F | F | T | T | T | T | T |
The final column (∼p∨q)∧(∼p∧∼q) shows the overall truth values for the given statement.
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL REASONING EXERCISE - illusration 1
1 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL REASONING EXERCISE - illusration 3
1 Videos
- MATHEMATICAL INDUCTION BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise
30 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
In the truth table for the statement (~p⇒~q)∧(~q⇒~p), the last column has the truth value in the following order
ATTTFBFTTFCTFFTDTTTTIn the truth table for the statements (p→q)↔(~p∨q), the last column has the truth value in the following order
ATTTTBFTFTCTTFFDFFFF
Write down the truth tables for the following statements :
(p∧q)⇒~p (ii)(p∧q)⇒(p∨q)
View SolutionWrite the truth table of AND gate.
View SolutionGiven the truth table of ~p∨q
View SolutionWrite the truth table for the following circuit:
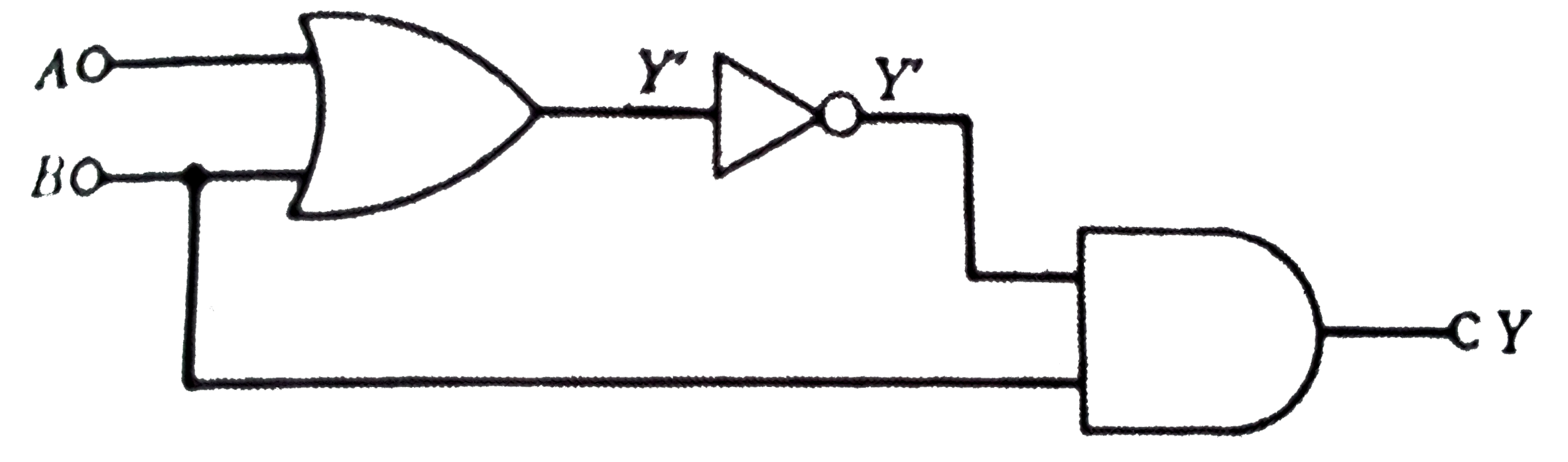
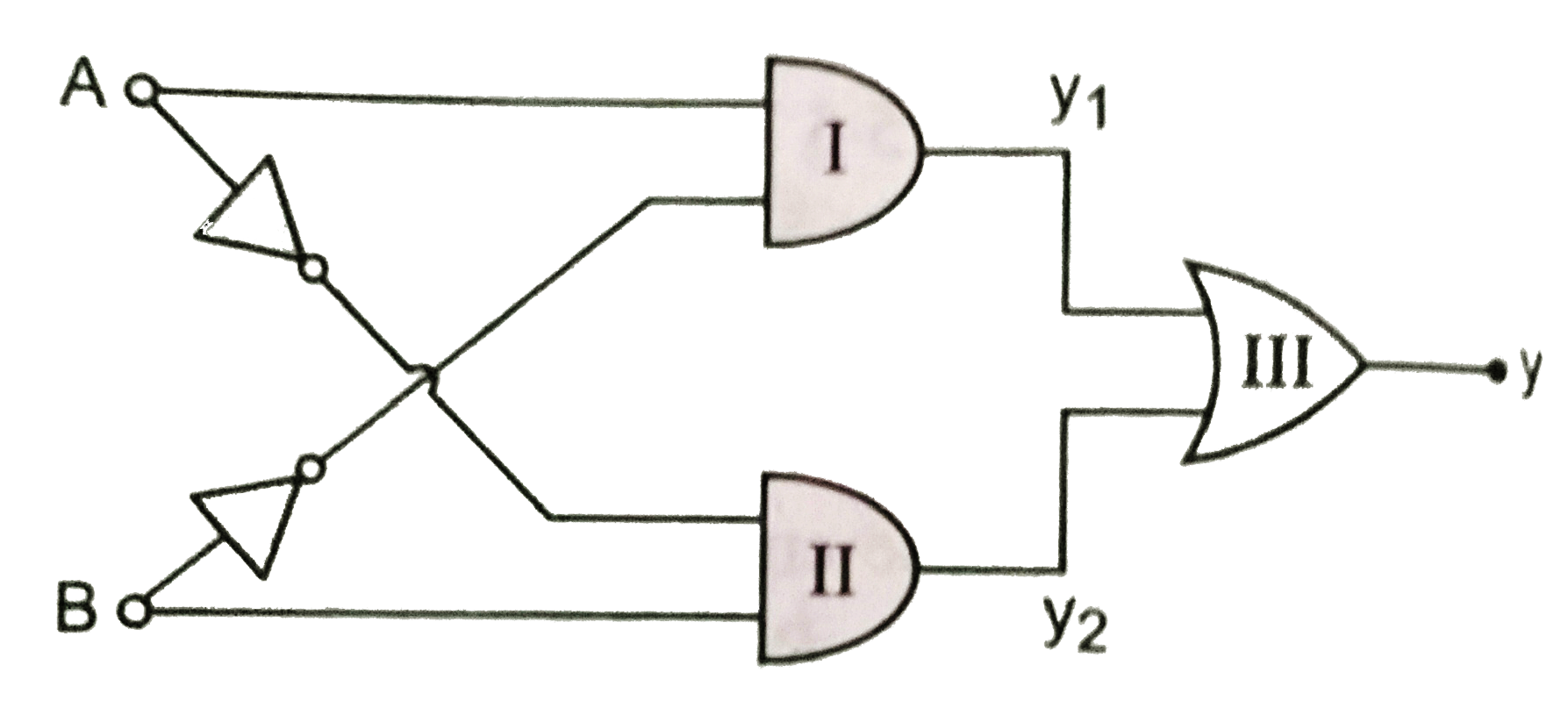
View SolutionWrite the truth table for the circuit shown in Fig.
View SolutionConstruct the truth table for the statement p→[q→(p∧q)]p→[q→(p∧q)]. Interpret the result.
View Solution
