Write the coordinate of each of the points P,Q, R,S,T and o from the figure

Here, points P and S lie in I quadrant so their both coordinate will be positive. Now, perpendicular distance of P from both axes is 1, so coordinate of P are (1,1) . Also, perpendicular distance of S from X-axis is 1 and from Y-axis is 2, so coordinate of S are (2,1). Point Q lies on X-axis in negative direction so its y-coordinate will be zero and x-coordinate will be -3 . So, coordinate of Q are (-3,0) . Point R lies in III quadrant , so its both coordinates will be negative .Now, its perpendicular distance from X-axis is 3 and from Y-axis is 2, so coordinates of point R are(-2,-3).
Point R lies in IV quadrant , so its x-coordinate will be positive and y-coordinate will be negative. Now, its perpendicular distance from X-axis is 2 and from Y-axis is 4, so coordinate of T are (4,-2) . Point O is the intersection of both axes, so it is the origin and its coordinate are O(0,0).
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.4 Long Answer Type Questions5videos
COORDINATE GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.2 Very Short Answer Type Questions1videos
COORDINATE GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions8videos
HERON'S FORMULA
Similar Questions
Knowledge Check
- Question 1 - Select One
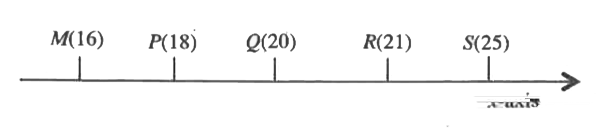
Which one of the following points in the figure is the median of the points M, P, Q, R and S?AMBPCQDR
Show that the relation R in the set A of points in a plane given by R={(P,Q):distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set o
View SolutionThe coordinates of the point P are (−3, 2) . Find the coordinates of the point Q which lies on the line joining P and origin such that OP=OQ .
View SolutionA straight line through the vertex P of a triangle PQR intersects the side QR at the points S and the cicumcircle of the triangle PQR at the point T. If S is not the center of the circumcircle, then 1PS+1ST<2√QS×SR 1PS+1ST>2√QS×SR 1PS+1ST<4QR 1PS+1ST>4QR
View SolutionLet P and Q be any two points. Find the coordinates of the point R which divides PQ externally in the ratio 2:1 and verify that Q is the mid point of PR .
View SolutionPoints P, Q, R and S divide the line segment joining the points A(1, 2) and B(6,7) in 5 equal parts. Find the coordinates of the points P, Q and R .
View SolutionABCD is a tetrahedron and O is any point. If the lines joining O to the vertices meet the opposite faces at P,Q,RandS, prove that OPAP+OQBQ+ORCR+OSDS=1.
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are a. (43,3) b. (3,23) c. (3,43) d. (43,23)
View Solution