Write the negation of the following:
If the determinant of a system of linear equations is zero, then either the system has no solution or it has an infinite number of solution.
To find the negation of the statement "If the determinant of a system of linear equations is zero, then either the system has no solution or it has an infinite number of solutions," we can follow these steps:
1. Identify the Components of the Statement:
- Let P: "The determinant of a system of linear equations is zero."
- Let Q: "The system has no solution."
- Let R: "The system has an infinite number of solutions."
The original statement can be expressed as:
P⟹(Q∨R)
2. Write the Negation:
The negation of an implication A⟹B is given by:
¬(A⟹B)≡A∧¬B
Applying this to our statement:
¬(P⟹(Q∨R))≡P∧¬(Q∨R)
3. Apply De Morgan's Law:
According to De Morgan's Law, the negation of a disjunction is:
¬(Q∨R)≡¬Q∧¬R
Therefore, we can rewrite our negation as:
P∧(¬Q∧¬R)
This can be rearranged as:
P∧¬Q∧¬R
4. Translate Back to Words:
Now, substituting back the definitions of P, Q, and R:
- P: "The determinant of a system of linear equations is zero."
- ¬Q: "The system has at least one solution."
- ¬R: "The system does not have an infinite number of solutions."
Thus, the negation of the original statement is:
"The determinant of a system of linear equations is zero, and the system has at least one solution, and it does not have an infinite number of solutions."
Final Answer:
The negation of the statement is:
"The determinant of a system of linear equations is zero, and the system has at least one solution, and it does not have an infinite number of solutions."
- Let P: "The determinant of a system of linear equations is zero."
- Let Q: "The system has no solution."
- Let R: "The system has an infinite number of solutions."
P⟹(Q∨R)
The negation of an implication A⟹B is given by:
¬(A⟹B)≡A∧¬B
Applying this to our statement:
¬(P⟹(Q∨R))≡P∧¬(Q∨R)
According to De Morgan's Law, the negation of a disjunction is:
¬(Q∨R)≡¬Q∧¬R
Therefore, we can rewrite our negation as:
P∧(¬Q∧¬R)
This can be rearranged as:
P∧¬Q∧¬R
Now, substituting back the definitions of P, Q, and R:
- P: "The determinant of a system of linear equations is zero."
- ¬Q: "The system has at least one solution."
- ¬R: "The system does not have an infinite number of solutions."
"The determinant of a system of linear equations is zero, and the system has at least one solution, and it does not have an infinite number of solutions."
The negation of the statement is:
"The determinant of a system of linear equations is zero, and the system has at least one solution, and it does not have an infinite number of solutions."
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (1)(MULTIPLE CHOICE QUESTIONS)29videos
MATHEMATICAL REASONING
- BOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (1)(FILL IN THE BLANKS)22videos
MATHEMATICAL REASONING
- BOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise3videos
LOGARITHMS AND SURDS
- BOOK - ML KHANNACHAPTER - MATRICESEXERCISE - COMPREHENSION3videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
If the system of linear equations px+3y=9and4x+py=8 has unique solution, then
Ap=−+2√3Bp≠−+3√2Cp≠−+2√3Dp=−+3√2 - Question 2 - Select One
Which of the following system of equation has infinitely many solutions ?
A2x+3y=12,4x+6y=12Bx−3y=10,2x−6y=20Cx=4,y=3D3x−4y=0,3x+4y=0
If the system of linear equations is inconsistent, then the solution set is infinite. (Agree/Disagree)
View SolutionSolution of system of linear equations by determinant method| Condition for consistency
View SolutionA non homogeneous system of linear equations in three variables AX=D has unique solution if
View SolutionFor what value of K, the system of equation 2x+4y+16=0 and 3x+Ky+24=0 has an infinite number of solutions.
View SolutionDetermine the system of linear equation for which the solution set is the shaded region in the following figure
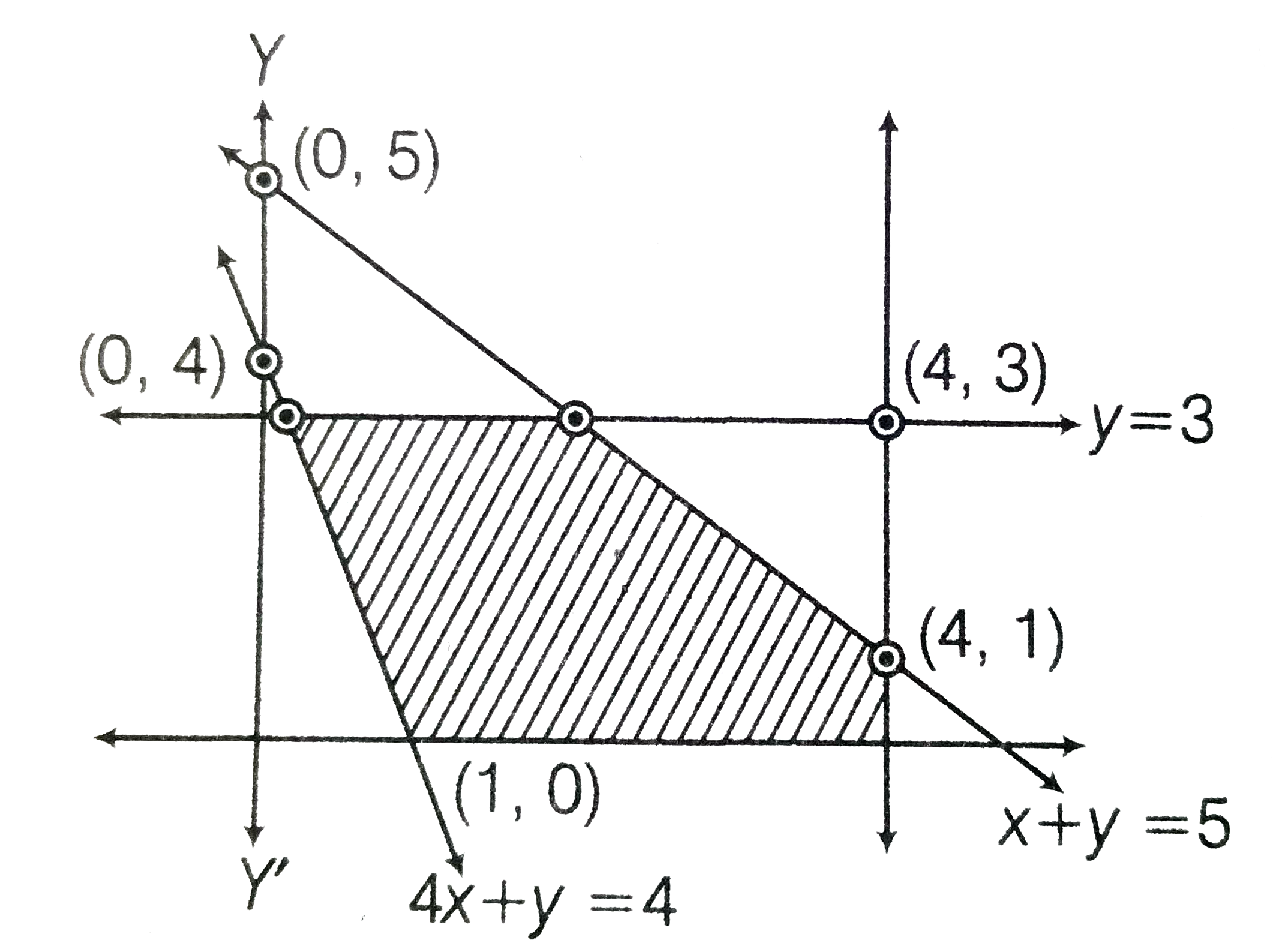 View Solution
View SolutionShow that the system of equations.
2x−3y=5,6x−9y=15.
has an infinite number of solutions.View Solution

