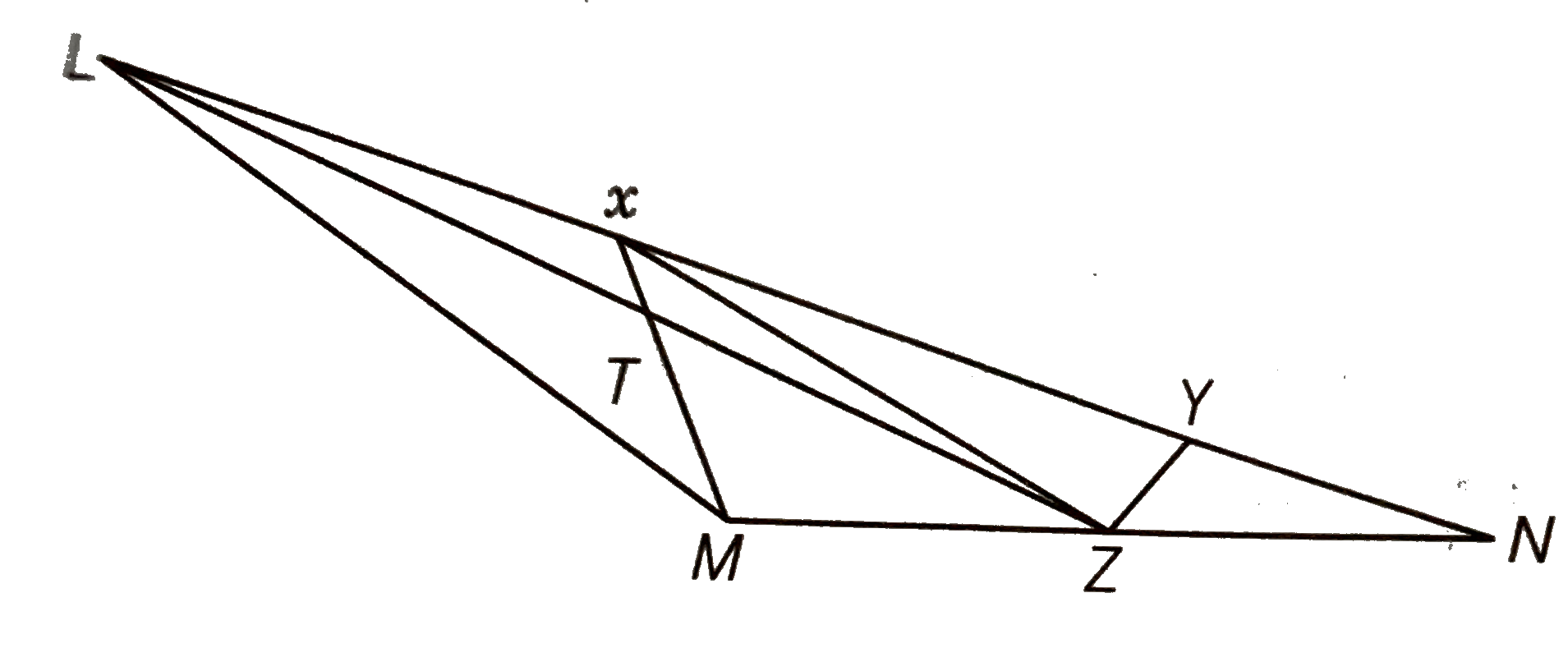
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that ar(ΔLZY)=ar(MZYX).
△PSMand△QSM have the same base SM and lie between the same parallels PQ and MS.
∴ar(△PSM)=ar(△QSM)
⇒ar(△PSM)+ar(△MSN)=ar(△QSM)+ar(△MSN)
⇒ar(△PSN)=ar(QSNM).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
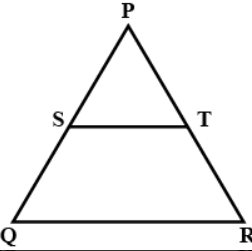
PQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
In△PQR,wehavePQ=PR
View SolutionIn figure, PQR is a triangle in which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT.
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionABCD is a trapezium with AB||DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
View SolutionIn the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.

View SolutionABCD is a trapezium with AB || DC.A parallel to AC cuts the line AB at X and BC at Y. Prove that ar (ADX) = ar (ACY)
View SolutionLex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that TX2=TB x TC
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View Solution
